【定义】单时期离散时间模型

基于《数理金融学引论—离散时间模型》；

第一部分笔记：单时期市场；

• 在有限样本空间 $\Omega$ 中，$\omega$ 为某一时间的一种可能状态，P($\omega_k$) 为状态 k 发生的概率。

$$\begin{aligned} \Omega = \{\omega_1,\omega_2,...,\omega_K\}\\ P(\omega_k)>0 \ , \ \sum_{k=1}^K p(\omega_k)=1 \end{aligned}$$

• 银行账户过程（Bank Account Process）B
• 价格过程（Price Process）S
• 交易策略（Trading Strategy）H

$$H_0 = x-\sum_{i=1}^{n}H_nS_n(0)$$

• 价值过程（Value Process）V

$$V_t \equiv H_0B_t + \sum_{n=1}^N H_nS_n(t) \ , \ t = 0,1$$

• 增益过程（Gains Process）G

$$\begin{aligned} \Delta S_n &\equiv S_n(1)-S_n(0)\\ G &\equiv V_1-V_0 \equiv H_0r + \sum_{n=1}^N H_n \Delta S_n \end{aligned}$$

• 折现价格过程（Discounted Price Process）S^*^

$$S_n^*(t) \equiv S_n(t)/B_t \ , \ t = 0,1$$

• 折现价值过程（Discounted Value Process）V^*^

$$V_t^* \equiv V_t/B_t \equiv H_0 + \sum_{n=1}^N H_nS_n^*(t) \ , \ t = 0,1$$

• 折现增益过程（Discounted Gains Process）G^*^

$$\begin{aligned} G^* &\equiv V_1^*-V_0^* \equiv \sum_{n=1}^N H_n \Delta S_n^*\\ G^* &\not\equiv G/B_t \ (\ V_0,V_1除的B_t不一样\ ) \end{aligned}$$

• 线性定价测度（Linear Pricing Measure）$\pi$

$$\begin{aligned} V_0^* &= \sum_\omega \pi(\omega)V_1^*(\omega) = \sum_\omega \pi(\omega)V_1(\omega)/B_1(\omega)\\ H_0 +& \sum_{n=1}^N H_nS_n^*(0) = \sum_\omega \pi(\omega)[H_0 + \sum_{n=1}^N H_nS_n^*(1)(\omega)] \end{aligned}$$

为满足线性条件使$\sum_\omega \pi(\omega)=1$ , 这样人们把 $\pi$ 解释成样本空间 $\Omega$ 上的一个概率测度

$$S_n^*(0) = \sum_\omega \pi(\omega)S_n^*(1)(\omega)$$

• 风险中性概率测度（Risk Neutral Probability）Q

$$\begin{aligned} &Q(\omega)>0 \ , \ E_Q[\Delta S_n^*]=0\\ E_Q[\Delta S_n^*] = &E_Q[S_n^*(1)-S_n^*(0)] = E_Q[S_n^*(1)]-S_n^*(0) \end{aligned}$$

与$\pi(\omega)$等价

$$\begin{aligned} \mathbb{W} &\equiv \{X\in \mathbb{R}^K:X = G^* 对于某一个交易策略H\}\\ \mathbb{A} &\equiv \{X\in \mathbb{R}^K:X \geqq0 ,X\not=0 \}\\ \mathbb{W} \cap \mathbb{A}&\not= \empty \ :\mathbb{W}的非负象限\\ \mathbb{W}^\perp &\equiv \{Y\in \mathbb{R}^K:X·Y=0 \ 对于所有X\in \mathbb{W}\}\\ \mathbb{P}^+ &\equiv \{X\in \mathbb{R}^K:X_1+...+X_K=1 ,X_1>0,...,X_K>0\} \end{aligned}$$

$$\begin{aligned} Q\in &\mathbb{W}^\perp \cap \mathbb{P}^+\\ Where \ E_Q[G^*]&=\sum_{n=1}^NH_nE_Q[S_n^*]=0 \end{aligned}$$

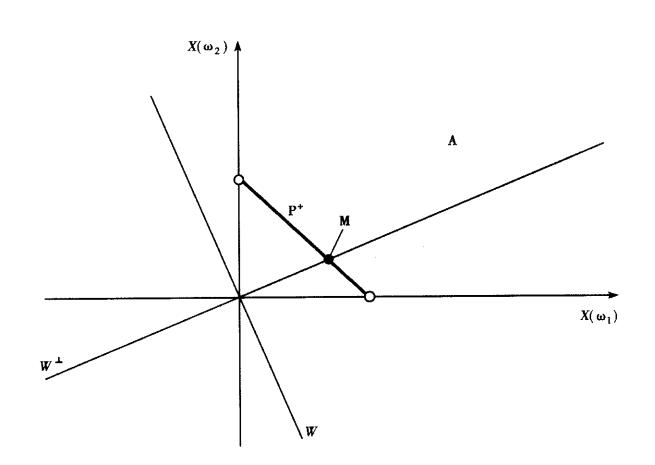
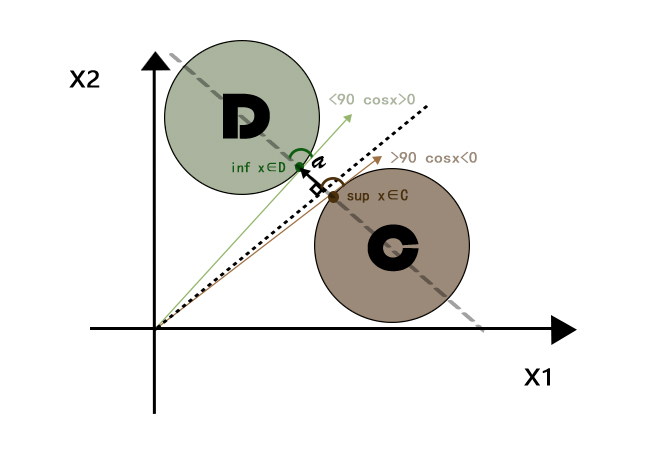
• 超平面分离定理（Separating hyperplane theorem）: 若 C , D为非空凸集，且 $C \cap D = \empty$，则存在 $a \not= 0 , b $ 使得 $$\begin{aligned} a^Tx&\leqq b \ for \ x\in C\\ a^Tx&\geqq b \ for \ x\in D\\ inf_{x\in D}a^Tx&\geqq sup_{x\in C}a^Tx \end{aligned}$$

可推导当$\mathbb{W}\cap\mathbb{A} = \empty$, 必有$\mathbb{W}^\perp\cap\mathbb{P}^+\not=\empty$, 且$\mathbb{W}^\perp=\lambda a$