【笔记】Inner product and Cross Product

对内积与外积基础性质进行简要陈述；

内积（Inner product，点乘）

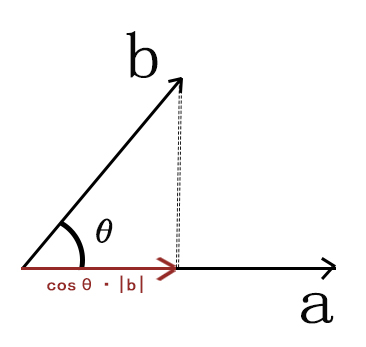
$a = [a_1,a_2,...,a_n] \qquad b = [b_1,b_2,...,b_n]$ $a·b = |a||b|Cos\angle(a,b)$

在几何中这个结果为b在a方向上的投影，若a与b正交，$a·b=0$
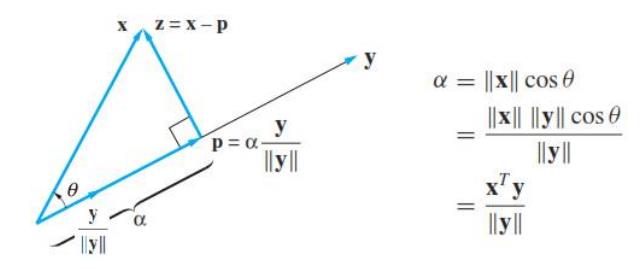
Scalar projrction of x onto y ：$\alpha=\frac{x^Ty}{||y||}$
Vector projection of x onto y : $P=\alpha\frac1{||y||}y=\frac{x^Ty}{y^Ty}y$

If $a=(a_1,a_2,a_3)$ and $b=(b_1,b_2,b_3)$. Then $a·b=a_1b_1+a_2b_2+a_3b_3$

证明：
- $|a-b|^2=|a|^2+|b|^2-2|a||b|Cos\angle(a,b)$
- $|a|^2=a_q^2+a_2^2+a_3^2,|b|^2=b_q^2+b_2^2+b_3^2$
- $|a-b|^2=(a_1-b_1)^2+(a_2-b_2)^2+(a_3-b_3)^2$
  $\begin{aligned} a·b&=|a||b|Cos\angle(a,b)\\ &=\frac12(|a|^2+|b|^2-|a-b|^2)\\ &=\frac12(a_q^2+a_2^2+a_3^2+b_q^2+b_2^2+b_3^2-(a_1-b_1)^2-(a_2-b_2)^2-(a_3-b_3)^2)\\ &=a_1b_1+a_2b_2+a_3b_3 \end{aligned}$

外积（Cross Product，叉乘）

$a = (x_1,y_1,z_1) \qquad b = (x_2,y_2,z_2)$ $a \times b = \begin{vmatrix} i & j & k \\ x_1 & y_1 & z_1 \\x_2 & y_2 & z_2 \end{vmatrix} = (y_1z_2-y_2z_1)i-(x_1z_2-x_2z_1)j+(x_1y_2-x_2y_1)k$

其中

$i = (1,0,0) \ j = (0,1,0) \ k = (0,0,1)$

得到结果向量

$a \times b = (y_1z_2-y_2z_1,-(x_1z_2-x_2z_1),x_1y_2-x_2y_1)$

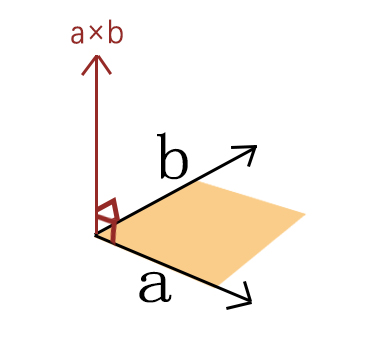
在几何中这个结果称为法向量，该向量垂直于a和b向量构成的平面

叉乘同时拥有其它基本性质：

$a \times a = 0$
$a \times b = -( b \times a)$
$(a + b)\times c = a \times c + b \times c$
$(a\times b)\times c\ne a\times(b\times c)$
$(a\times b)·c=a·(b\times c)$

可得到叉乘公式推导：

$\begin{aligned} u \times v =& (u_1i+u_2j+u_3k)\times(v_1i+v_2j+v_3k)\\ =&u_1v_1(i \times i)+u_1v_2(i \times j)+u_1v_3(i \times k)+\\ &u_2v_1(j \times i)+u_2v_2(j \times j)+u_2v_3(j \times k)+\\ &u_3v_1(k \times i)+u_3v_2(k \times j)+u_3v_3(k \times k)+ \end{aligned}$

同时因为

$i\times i = j\times j = k\times k = 0$ $\begin{cases} i\times j = k\\ j\times k = i\\ k\times i = j \end{cases} \ \begin{cases} j\times i = -k\\ k\times j = -i\\ i\times k = -j \end{cases}$

得到

$\begin{aligned} u\times v =& (u_2v_3-u_3v_2)i+(u_3v_1-u_1v_3)j+(u_1v_2-u_2v_1)k\\ =& \begin{vmatrix} u_2 & u_3 \\v_2 & v_3 \end{vmatrix}i - \begin{vmatrix} u_1 & u_3 \\v_1 & v_3 \end{vmatrix}j + \begin{vmatrix} u_1 & u_2 \\v_1 & v_2 \end{vmatrix}k\\ =& \begin{vmatrix} i & j & k\\u_1 & u_2 & u_3\\v_1 & v_2 & v_3 \end{vmatrix} \end{aligned}$

证明垂直：
$\begin{aligned} (u\times v)·w =& (u_2v_3-u_3v_2)w_1+(u_3v_1-u_1v_3)w_2+(u_1v_2-u_2v_1)w_3\\ =& \begin{vmatrix} w_1 & w_2 & w_3\\u_1 & u_2 & u_3\\v_1 & v_2 & v_3 \end{vmatrix} \end{aligned}$ $(u\times v)·u = \begin{vmatrix} u_1 & u_2 & u_3\\u_1 & u_2 & u_3\\v_1 & v_2 & v_3 \end{vmatrix}=u_1u_2v_3+u_2u_3v_1+u_3u_1v_2-u_3u_2v_1-u_2u_1v_3-u_1u_3v_2=0$ $(u\times v)·v = \begin{vmatrix} v_1 & v_2 & v_3\\u_1 & u_2 & u_3\\v_1 & v_2 & v_3 \end{vmatrix}=v_1u_2v_3+v_2u_3v_1+v_3u_1v_2-v_3u_2v_1-v_2u_1v_3-v_1u_3v_2=0$
$u$ $v$ is perpendicular to both $u$ and $v$.

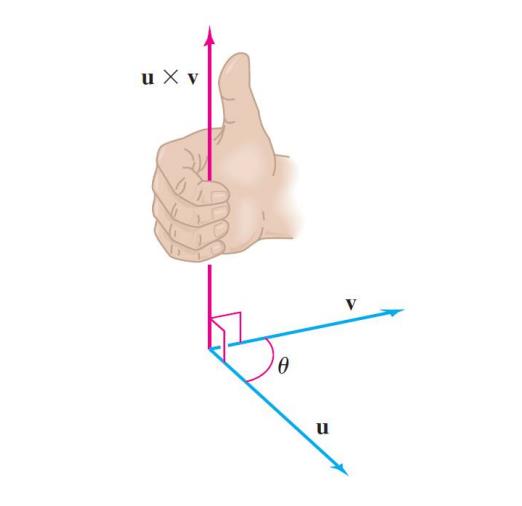
扩充

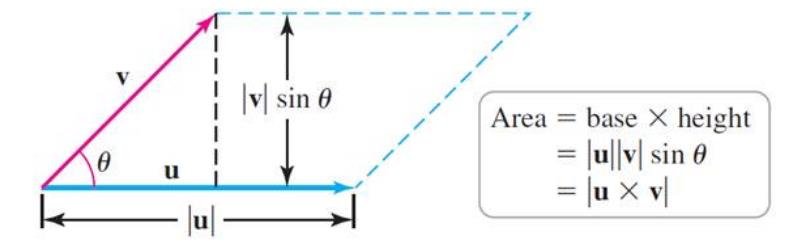
If $u=(u_1,u_2,u_3)$ and $v=(v_1,v_2,v_3)$. Then $|u\times v|=|u||v|Sin\angle(a,b)$

证明：
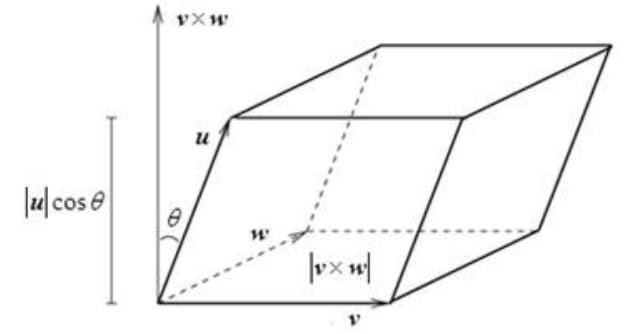
$\begin{aligned} |u\times v|^{2} &=(u_{2} v_{3}-u_{3} v_{2})^{2}+(u_{3} v_{1}-u_{1} v_{3})^{2}+(u_{1} v_{2}-u_{2} v_{1})^{2} \\ &=(u_{2} v_{3})^{2}-2(u_{2} v_{3})(u_{3} v_{2})+(u_{3} v_{2})^{2} \\ &+(u_{3} v_{1})^{2}-2(u_{3} v_{1})(u_{1} v_{3})+(u_{1} v_{3})^{2} \\ &+(u_{1} v_{2})^{2}-2(u_{1} v_{2})(u_{2} v_{1})+(u_{2} v_{1})^{2} \\ &=(u_{1} v_{1})^{2}+(u_{1} v_{2})^{2}+(u_{1} v_{3})^{2}+(u_{2} v_{1})^{2}+(u_{2} v_{2})^{2}+(u_{2} v_{3})^{2}+(u_{3} v_{1})^{2}+(u_{3} v_{2})^{2}+(u_{3} v_{3})^{2} \\ &-[(u_{1} v_{1})^{2}+(u_{2} v_{2})^{2}+(u_{3} v_{3})^{2}+2(u_{1} v_{1})(u_{2} v_{2})+2(u_{2} v_{2})(u_{3} v_{3})+2(u_{1} v_{1})(u_{3} v_{3})] \\ &=(u_{1}^{2}+u_{2}^{2}+u_{3}^{2})(v_{1}^{2}+v_{2}^{2}+v_{3}^{2})-(u_{1} v_{1}+u_{2} v_{2}+u_{3} v_{3})^{2} \\ &=|u|^{2}|v|^{2}-(u \cdot v)^{2} \\ &=|u|^{2}|v|^{2}-|u|^{2}|v|^{2}Cos^2\angle(a,b)\\ &=|u|^{2}|v|^{2}Sin^2\angle(a,b) \end{aligned}$

$|v\times w||u|Cos\angle(a,b)=u·(v\times w)=\begin{vmatrix}u_1 & u_2 & u_3\\v_1 & v_2 & v_3\ w_1 & w_2 & w_3\end{vmatrix}$

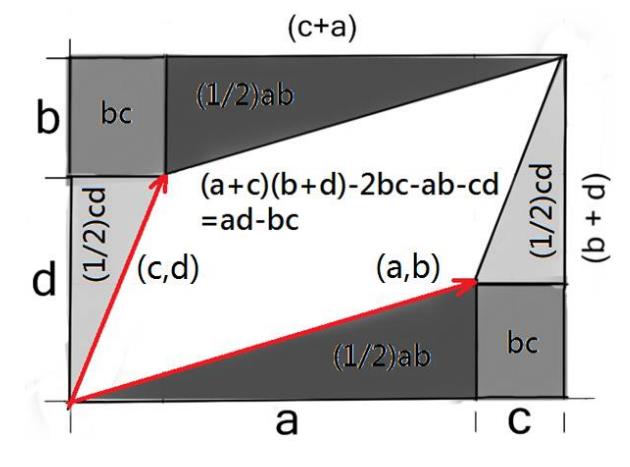
The area of the parallelogram generated by the vectors $(a, b)$ and $(c, d)$ is $det\left(\matrix{a&b\\c&d}\right)$

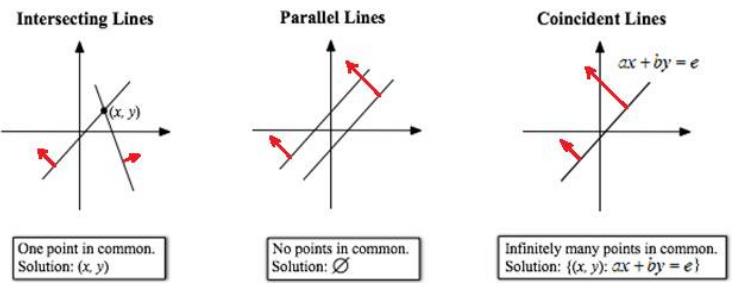
$\left\{\matrix{ax+by=e\\cx+dy=f}\right.$ ，只有在 $det\left(\matrix{a&b\\c&d}\right)\ne0$ 时才有解，解为 $\left(\matrix{a&b\\c&d}\right)^{-1}\left(\matrix{e\\f}\right)$