【笔记】Change of Measure

基于B站up Jerry Xu 的视频《概率测度变换》系列的笔记

Section 1：Preliminary of Probability Theory

1. Probability Space

$$(\Omega,\mathcal{F},\mathbb{P})$$

• Sample Space (可能出现的结果)：$\Omega$

  • $\Omega=\{\omega_1,\omega_2,…\}$
  • $\Omega =\omega_i, i\in I(index set)$，无限多不可数
  • Random Variable $X(\omega)$定义在$\Omega$上
    • $X：\Omega \to \mathbb{R}^K$
    • $X^{-1}(B)=\{\omega\in\Omega:X(\omega)\in B\}\in \mathcal{F} for all$
      • Borel sets：$B\in\mathscr{B}(\mathbb{R}^K)$

• $\sigma$-algebra (all measurable events)：$\mathcal{F}$

  • $\varnothing \in \mathcal{F}$
  • $A \in \mathcal{F} \Rightarrow A^C \in \mathcal{F}$
  • $A_1,A_2,…\in\mathcal{F}\Rightarrow\cup_{n=1}^\infty A_n\in\mathcal{F}$
  • Events are subset of $\Omega$

• Probability measure (all events will be assigned a value)：$\mathbb{P}$

  • $\mathbb{P}(\Omega)=1$

  • $If A_1,A_2,… are disjoint sets$

    $\Rightarrow \mathbb{P}(\cup_{n=1}^\infty A_n)=\sum_{n=1}^\infty\mathbb{P}(A_n)$

  • $\mathbb{P}$能给$\mathcal{F}$中每一个事件都映射到闭区间0到1上，所以概率测度定义域是$\sigma$域

    • $\mathbb{P}：\Omega \to [0,1]$

De Morgan’s law

$$(A\cap B)^C=A^C\cup B^C,\ (A\cup B)^C=A^C\cap B^C$$

2. Other Definition

期望

• Countable Infinite

$$\mathbb{E}X=\sum_{k=1}^\infty X(\omega_k)\mathbb{P}(\omega_k)$$

• Uncountable Infinite

$$\begin{align} \mathbb{E}X&=\int_\Omega X(\omega)d\mathbb{P}(\omega) (Leb\ Integral)\\ &=\int_{-\infty}^\infty x\underbrace{f(x)}dx=\int_{-\infty}^\infty xd\underbrace{F(x)}\\ &\ \qquad\qquad pdf\ \qquad\qquad\quad\quad cdf \end{align}$$

Riemann积分(upper)&Lebesgue积分(lower)

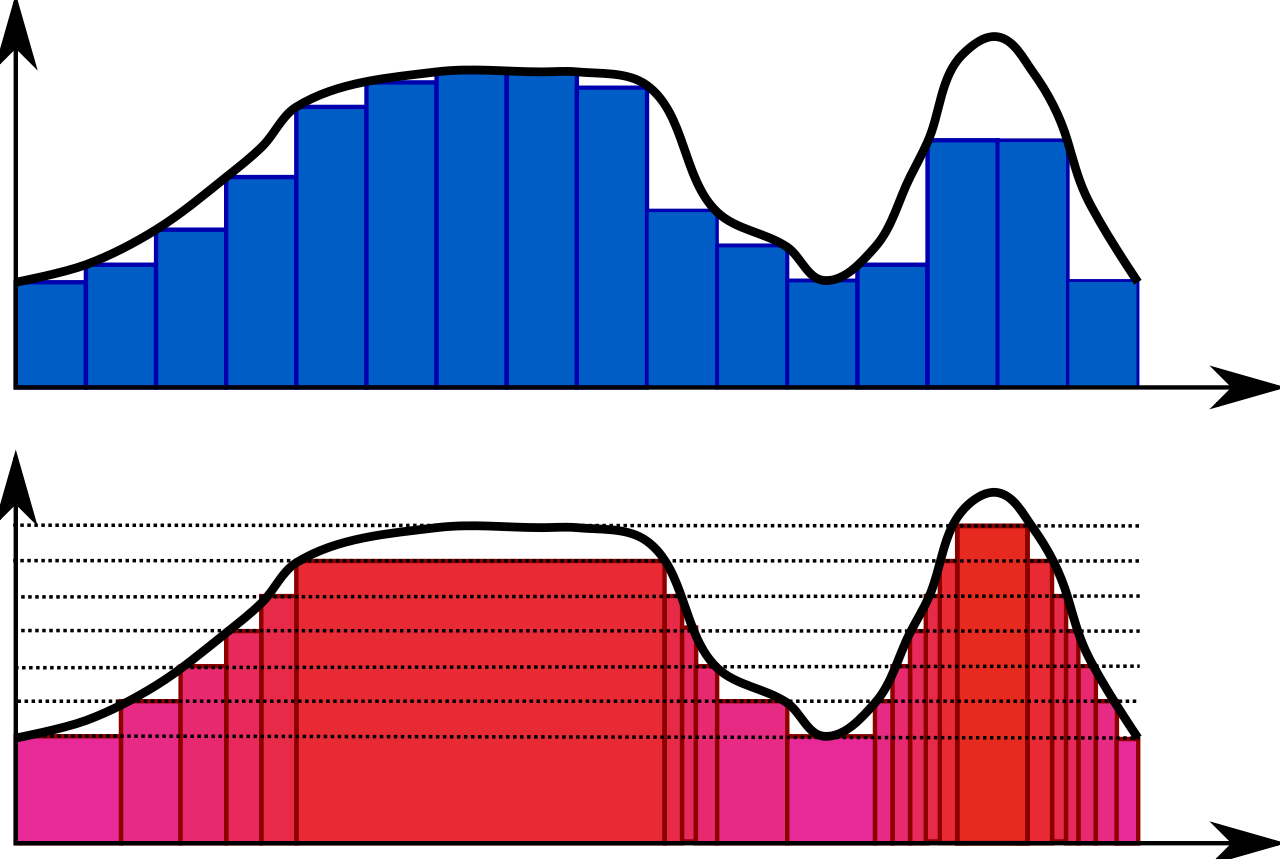
Indicator function (示性函数)

$$\mathbb{I}_A(\omega)=\begin{cases}1&,\omega\in A\\0&,\omega\not\in A\end{cases}$$ $$\mathbb{E}[\mathbb{I}_A(\omega)]=\mathbb{P}(\omega\in A)$$

积分

For $A\subset\Omega, A\in\mathcal{F}$

$$\int_AX(\omega)d\mathbb{P}(\omega)=\int_\Omega\mathbb{I}_A(\omega)X(\omega)d\mathbb{P}(\omega)$$

For $A\subset\Omega, B\subset\Omega, A,B\in\mathcal{F}$

and $A \cap B = \varnothing$

$$\begin{align} \int_{A\cup B}X(\omega)d\mathbb{P}(\omega)&=\int_\Omega\mathbb{I}_{A\cup B}(\omega)X(\omega)d\mathbb{P}(\omega)\\ &=\int_\Omega\mathbb{I}_A(\omega)X(\omega)d\mathbb{P}(\omega)+\int_\Omega\mathbb{I}_B(\omega)X(\omega)d\mathbb{P}(\omega) \end{align}$$

($A \cap B = \varnothing$)	$\mathbb{I}_A$	$\mathbb{I}_B$	$\mathbb{I}_{A\cup B}$
$A$	1	0	1
$B$	0	1	1
$A\cup B$	0	0	0

3. Change of Measure

测度

• 测度$\mathbb{P}$：真实世界测度

• 测度$\mathbb{Q}$：单个风险中性测度 (股票过程) 多个等价鞅测度 (债券过程)

Radon-Nikodym Derivative

Let $Z\ge 0$, with

$$\mathbb{E}^\mathbb{P}[Z(\omega)]=1$$

For $A\in \mathcal{F}$, define

$$\mathbb{Q}(A)=\int_AZ(\omega)d\mathbb{P}(\omega)$$ $$\mathbb{Q}(A)=\sum_{\omega\in A}\mathbb{Q}(\omega)=\sum_{\omega\in A}\mathbb{P}(\omega)Z(\omega)$$

Then $\mathbb{Q}$ is a prob measure.

Furtheremore, if $X\ge 0$, then

$$\mathbb{E}^\mathbb{Q}[X]=\mathbb{E}^\mathbb{P}[XZ]$$

if $Z> 0$, then

$$\mathbb{E}^\mathbb{Q}[\frac{X}{Z}]=\mathbb{E}^\mathbb{P}[X]$$

4. Example

Question：we have $X(\omega)=\omega\sim N^\mathbb{P}(0,1)$ . Set $Y(\omega)=X(\omega)+\theta (\theta>0)$ . So it follow $N^\mathbb{P}(\theta,1)$ . Build a Probability measure $\mathbb{Q}$ and make $Y$ follow $N^\mathbb{Q}(0,1)$ . Find the Radon-Nikodym Derivative.

$$Z(\omega)=\frac{d\mathbb{Q}(\omega)}{d\mathbb{P}(\omega)}$$

Recall that the PDF and CDF of Standard normal distribution：

PDF

$$\phi(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}},\ x\in \mathbb{R}$$

CDF

$$\Phi(x)=\int_{-\infty}^x\frac{1}{\sqrt{2\pi}}e^{-\frac{s^2}{2}}ds$$

Under $\mathbb{P}: X\sim N^\mathbb{P}(0,1)$, we have:

$$\begin{align} \Delta\mathbb{P}(l)&=\mathbb{P}(l\leq\omega\leq l+\Delta l)\\ &= \Phi(l+\Delta l)-\Phi(l) \end{align}$$

Under $\mathbb{Q}: Y\sim N^\mathbb{Q}(0,1)$, we have:

$$\begin{align} \Delta\mathbb{Q}^*(l)&=\mathbb{Q}(l\leq Y(\omega)\leq l+\Delta l)\\ &=\mathbb{Q}(l-\theta\leq\omega\leq l+\Delta l-\theta)\\ &=\Phi(l+\Delta l)-\Phi(l) \end{align}$$

Set $l\to l+\theta$

$$\begin{align} \Delta\mathbb{Q}(l)=\Delta\mathbb{Q}^*(l+\theta)&=\mathbb{Q}(l\leq\omega\leq l+\Delta l)\\ &=\Phi(l+\Delta l+\theta)-\Phi(l+\theta) \end{align}$$

Solving the function

$$\begin{align} Z(l)&=\frac{d\mathbb{Q}(l)}{d\mathbb{P}(l)}\\ &=\lim_{\Delta l\to 0}\frac{\Delta\mathbb{Q}(l)}{\Delta\mathbb{P}(l)}\\ &=\lim_{\Delta l\to 0}\frac{\Phi(l+\Delta l+\theta)-\Phi(l+\theta)}{\Phi(l+\Delta l)-\Phi(l)}\\ & (\frac{0}{0})\ 洛必达法则\\ &=\lim_{\Delta l\to 0}\frac{\phi(l+\Delta l+\theta)}{\phi(l+\Delta l)}\\ &=\frac{\phi(l+\theta)}{\phi(l)} \end{align}$$

so

$$\begin{align} Z(\omega)&=\frac{\phi(\omega+\theta)}{\phi(\omega)}\\ &=\frac{\frac{1}{\sqrt{2\pi}}e^{-\frac{(\omega+\theta)^2}{2}}}{\frac{1}{\sqrt{2\pi}}e^{-\frac{\omega^2}{2}}}\\ &=exp(-\frac{(\omega+\theta)^2}{2}+\frac{\omega^2}{2})\\ &=exp(-\frac{\theta^2}{2}-X(\omega)\theta) \end{align}$$

在随机变量中 $Z(\omega)$ 为 exponential martingale (指数鞅)

$$dW_t^\mathbb{P}=dW_t^\mathbb{Q}-\theta_tdt,\ \theta_t=\frac{\mu-r}{\sigma}$$

真实世界中

$$\mathbb{P}:dS_t=\mu S_tdt+\sigma S_tdW_t^\mathbb{P}$$

风险中性世界中

$$\begin{align} \mathbb{Q}:dS_t&=\mu S_tdt+\sigma S_t(dW_t^\mathbb{Q}-\theta_tdt)\\ &=\mu S_tdt+\sigma S_tdW_t^\mathbb{Q}-S_t(\mu-r)dt\\ &=r S_tdt+\sigma S_tdW_t^\mathbb{Q} \end{align}$$

Section 2：Girsanov’s Theorem

1. Conditional Expection

$\mathscr{G}$ is a sub-$\sigma$-algebra of $\mathcal{F}$. $X$ is a nonnegative & integrable r.v. The conditiond expextation of $X$ given $\mathscr{G}$, denoted $\mathbb{E}[X|\mathscr{G}]$, is any r.v. that satisfies：

• $\mathbb{E}[X|\mathscr{G}]$ is $\mathscr{G}$-measurable
• $\int_A \mathbb{E}[X|\mathscr{G}]d\mathbb{P}(\omega)=\int_AX(\omega)d\mathbb{P}(\omega), for \forall A\in\mathscr{G}$ : Partical Averaging

Properties

1. Pull out property: If $X$ is a $\mathscr{G}$-measureable, then

   $$\mathbb{E}[XY|\mathscr{G}]=X\mathbb{E}[Y|\mathscr{G}]$$

2. Tower property (or Iteration): If $\mathcal{H}$ is a sub-$\sigma$-algebra of $\mathscr{G}$

   $$\mathbb{E}[\mathbb{E}[X|\mathscr{G}]|\mathcal{H}]=\mathbb{E}[X|\mathcal{H}]$$

Radon-Nikodym Derivative Process

$$Z(t)=\mathbb{E}[Z|\mathcal{F}(t)],\ 0\leq t\leq T$$

1. $Z(t)$ is a martingale ($0\leq s\leq t\leq T$)

   $$\begin{align} \mathbb{E}[Z(t)|\mathcal{F}(s)]&=\mathbb{E}[Z(t)|\mathcal{F}(s)]\\ &=\mathbb{E}[\mathbb{E}[Z|\mathcal{F}(t)]|\mathcal{F}(s)]\\ &=\mathbb{E}[Z|\mathcal{F}(s)]\\ &=Z(s) \end{align}$$

2. $Z(t)$ is Radon-Nikodym Derivative ($Y$ is $\mathcal{F}(t)$-measureable)

   $$\begin{align} \mathbb{E}^\mathbb{Q}[Y]&=\mathbb{E}^\mathbb{P}[YZ]\\ &=\mathbb{E}^\mathbb{P}[\mathbb{E}^\mathbb{P}[YZ|\mathcal{F}(t)]]\\ &=\mathbb{E}^\mathbb{P}[Y\mathbb{E}^\mathbb{P}[Z|\mathcal{F}(t)]]\\ &=\mathbb{E}^\mathbb{P}[YZ(t)] \end{align}$$

3. $\mathbb{Q}^\mathbb{P}[Y|\mathcal{F}(s)]=\frac{1}{Z(s)}\mathbb{E}^\mathbb{P}[YZ(t)|\mathcal{F}(s)]$ (Right hand side is the conditiond expextation of $Y$)

   • $\frac{1}{Z(s)}\mathbb{E}^\mathbb{P}[YZ(t)|\mathcal{F}(s)]$ is $\mathcal{F}(s)$-measureable
   • For any $A \in \mathcal{F}(s)$, we have $\int_AY(\omega)d\mathbb{Q}(\omega)=\int_A \frac{1}{Z(s)}\mathbb{E}^\mathbb{P}[YZ(t)|\mathcal{F}(s)]d\mathbb{Q}(\omega)$
   $$\begin{align} RHS&=\int_\Omega \mathbb{I}_A(\omega)\frac{1}{Z(s)}\mathbb{E}^\mathbb{P}[YZ(t)|\mathcal{F}(s)]d\mathbb{Q}(\omega)\\ &=\mathbb{E}^\mathbb{Q}[\mathbb{I}_A(\omega)\frac{1}{Z(s)}\mathbb{E}^\mathbb{P}[YZ(t)|\mathcal{F}(s)]]\\ &=\mathbb{E}^\mathbb{P}[\mathbb{I}_A(\omega)\mathbb{E}^\mathbb{P}[YZ(t)|\mathcal{F}(s)]]\\ &=\mathbb{E}^\mathbb{P}[\mathbb{E}^\mathbb{P}[\mathbb{I}_A(\omega)YZ(t)|\mathcal{F}(s)]]\\ &=\mathbb{E}^\mathbb{P}[\mathbb{I}_A(\omega)YZ(t)]\\ &=\mathbb{E}^\mathbb{Q}[\mathbb{I}_A(\omega)Y]\\ &=\int_\Omega\mathbb{I}_A(\omega)Yd\mathbb{Q}(\omega)\\ &=\int_A Yd\mathbb{Q}(\omega)=LHS \end{align}$$

4. levy’s theorem：Let $M(t)$, $t\ge 0$, be a martingale, relative to$\mathcal{F}(t)$, $t\ge 0$. Assume $M(0)=0$, $M(T)$ has contiunous paths and quadratic variation = t ( 二次变差 ) for all $t\ge 0$. $\Rightarrow M(t)$ is a Brownian Motion.

   • 当 $\{t_i^n\}_{i=0}^n$ 遍取 $[0,t]$ 的分割，其模 $\delta_n=max_{0\leq i\leq n-1}\{t_{i+1}^n-t_i^n\}\to 0$时，依概率收敛意义下的极限

     $$[B,B](t)=[B,B]([0,t])=\lim_{\delta_n\to0}\sum_{i=0}^{n-1}|B(t_{i+1}^n)-B(t_i^n)|^2$$

   • BM 只有 $dW(t)dW(t)=dt$ 会在一单位时间内积累一单位二次变差. $dtdt=dtdW(t)=0$

2. Girsanov

Let $W(t)$ be a BM on $(\Omega,\mathcal{F},\mathbb{P})$ and let $\mathcal{F}(t)$ be a filtration. For this BM, let $\Theta(t)$ be an adopted process. Define

$$Z(t)=exp(-\int_0^t\Theta(u)dW(u)-\frac{1}{2}\int_0^t\Theta^2(u)dv)$$ $$\tilde{W}(t)=W(t)+\int_0^t\Theta(u)du$$

or

$$Z(t)=exp(\int_0^t\Theta(u)dW(u)-\frac{1}{2}\int_0^t\Theta^2(u)dv)$$ $$\tilde{W}(t)=W(t)-\int_0^t\Theta(u)du$$

Set $Z=Z(T)$. Then $\mathbb{E}Z=1$, $Z\ge 0$

Where $\mathbb{Q}$ given by

$$\mathbb{Q}=\int_AZ(\omega)d\mathbb{P}(\omega),\ for\ \forall A\in \mathcal{F}$$

The process $\tilde{W}(t)$ is a BM

Prove

1. $\mathbb{E}Z=1$

   Set

   $$X(t)=-\int_0^t\Theta(u)dW(u)-\frac{1}{2}\int_0^t\Theta^2(u)dv$$ $$\begin{align} dZ(t)&=0+e^{X(t)}dX(t)+\frac{1}{2}e^{X(t)}dX(t)dX(t)\\ &=Z(t)(-\Theta(t)dW(t)-\frac{1}{2}\Theta^2(t)dt)+\frac{1}{2}Z(t)\Theta^2(t)dt\\ &=-\Theta(t)Z(t)dW(t) \end{align}$$

   $\Rightarrow Z(t)$ is a $\mathbb{P}$-martingale

   $$Z(t)=Z(0)-\int_0^t\Theta(u)Z(u)dW(u),\ Z(0)=exp(0)=1$$ $$\mathbb{E}Z=\mathbb{E}[Z(T)]=\mathbb{E}[Z(T)|\mathcal{F}(0)]=Z(0)=1$$

2. $\tilde{W}(t)Z(t)$ is a martingale

   $$\begin{align} d(\tilde{W}(t)Z(t))&=Z(t)d\tilde{W}(t)+\tilde{W}(t)dZ(t)+dZ(t)d\tilde{W}(t)\\ &=Z(t)[dW(t)+\Theta(t)dt]+\tilde{W}(t)[-\Theta(t)Z(t)dW(t)]...\\ &\quad ...+[-\Theta(t)Z(t)dW(t)][dW(t)+\Theta(t)dt]\\ &=Z(t)\Theta(t)dt+Z(t)dW(t)-\tilde{W}(t)\Theta(t)Z(t)dW(t)-\Theta(t)Z(t)dt\\ &=Z(t)(1-\tilde{W}(t)\Theta(t))dW(t) \end{align}$$

   $\Rightarrow \tilde{W}(t)Z(t)$ is a $\mathbb{P}$-martingale

3. $\tilde{W}(t)$ is a martingale $\mathbb{E}^\mathbb{Q}[\tilde{W}(t)|\mathcal{F(s)}]=\tilde{W}(s)$

   $$\begin{align} LHS&=\frac{1}{Z(s)}\mathbb{E}^\mathbb{P}[\tilde{W}Z(t)|\mathcal{F}(s)]\\ &=\frac{1}{Z(s)}\tilde{W}(s)Z(s)=\tilde{W}(s) \end{align}$$

   $\Rightarrow \tilde{W}(t)$ is a $\mathbb{Q}$-martingale

4. $\tilde{W}(0)=W(0)+\int_0^0\Theta(s)ds=0$

5. The both parts of $\tilde{W}(t)$ has contiunous paths.

6. $d\tilde{W}(t)=dW(t)+\Theta(t)dt$, where $dtdt=0$ accumulated zero quadratic variation.

   $$[\tilde{W},\tilde{W}](t)=[W,W](t)=t$$

7. $[3-6]\Rightarrow \tilde{W}(t)$ is a BM

---

Reference

1. Jerry Xu B站主页
2. 从Riemann积分到Lebesgue积分