基于B站 up 童哲校长的视频《傅里叶变换，拉普拉斯变换与小波变换》的笔记

复数基本复习

$Z=x+iy,\ i^2=-1$ $f(Z)=u(x,y)+iv(x,y),\ x,y,u,v\in\mathbb{R}$

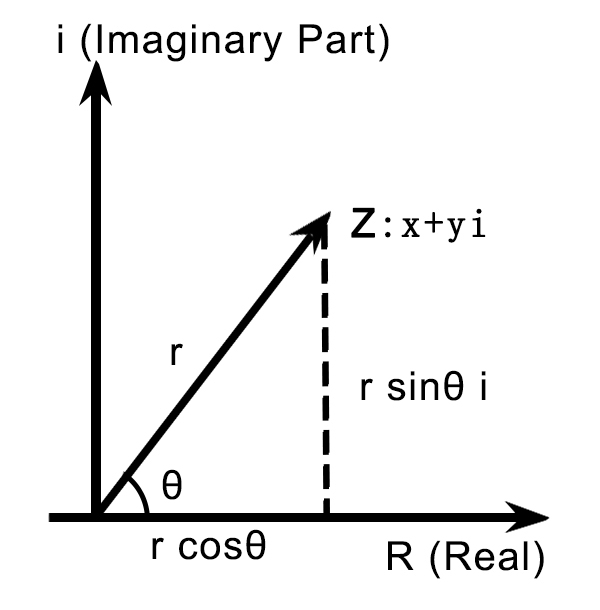
在图中虚部的解释

当一个实数乘 $i$，相当于把它逆时针旋转了90°
如果存在两个单位向量 $Z_1,Z_2$，并且它们的夹角呈90°，那么 $\frac{Z_1}{Z_2}=e^{i\frac{\pi}{2}}=i$

复数的极坐标表示

$Z=x+iy=re^{i\theta}=r(Cos\theta+iSin\theta)$

$e^{i\pi}=-1$ Euler Formula (欧拉公式)

共轭

$\bar{Z}=x-iy=re^{-i\theta}$ $Z+\bar{Z}=2cos\theta$ $Z-\bar{Z}=2isin\theta$

特性1

若 $f’(Z)$ 存在，$u,v$ 存在牵连关系，延 $x$轴 $y$轴接近的表达式相同

延 $x$轴：$Z-Z_0=\Delta x$

$\lim_{z-z_0}\frac{\Delta f(Z)}{\Delta Z}=\lim\frac{\Delta u+i\Delta v}{\Delta x}$

延 $y$轴：$Z-Z_0=i\Delta y$

$\lim_{z-z_0}\frac{\Delta f(Z)}{\Delta Z}=\lim\frac{\Delta u+i\Delta v}{i\Delta y}$

So we have Cauchy-Riemann Equations (柯西-黎曼方程)

$\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y},\ \frac{\partial v}{\partial x}=-\frac{\partial u}{\partial y}$

所有初等函数都满足此条件

特性2

当 $f(Z)$ 满足 C-R (柯西-黎曼)关系，只要知道边界的表达式，就能确定内部任意一个点的函数值

Step 1

当复变函数存在闭合的边界 $L$

$\oint_{L}f(Z)dZ=0$

证明

对于复变函数

$\begin{align} \oint_{L}f(Z)dZ&=\oint_{L}(u+iv)(dx+idy)\\ &=\oint_{L}(udx-vdy)+i\oint_{L}(vdx+udy) \end{align}$

Recall Green formula (格林公式)

$\oint_{L}(Pdx+Qdy)=\iint_L(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dxdy$ $\begin{align} \oint_{L}f(Z)dZ&=\oint_{L}(udx-vdy)+i\oint_{L}(vdx+udy)\\ &=\iint_L(-\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y})dxdy+i\iint_L(\frac{\partial u}{\partial x}-\frac{\partial v}{\partial y})dxdy \end{align}$

According to Cauchy-Riemann Equations

$\oint_{L}f(Z)dZ=0+0=0$

Step 2

求 $Z_0$ 点上的函数值

$f(Z_0)=\frac{1}{2\pi i}\oint_{L}\frac{f(Z)}{Z-Z_0}dZ$

证明

以 $Z_0$ 为圆心，取一个 $l$ 为边界，$\delta$为半径的圆. 此时我们有

$\oint_{L}f(Z)dZ=\oint_{l}f(Z)dZ=0$

$\oint_{L-l}f(Z)dZ=0$

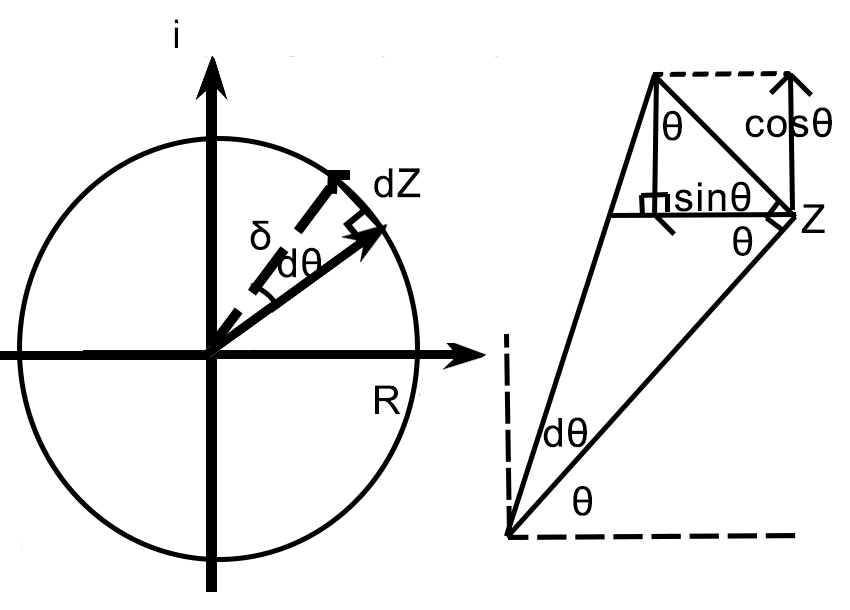
对边界求积时的 $dZ$ 相当于在边界上走一步

$dZ=\delta(-Sin\theta d\theta+iCos\theta d\theta)$ $Z-Z_0=\delta(Cos\theta+iSin\theta)$ $\frac{dZ}{Z-Z_0}=id\theta$

$\theta\in[0,2\pi]$

$\oint_{L} id\theta =2\pi i$

当 $\delta \to 0$, $Z\to Z_0$

$\frac{f(Z_0)}{2\pi i}\oint_{L}\frac{dZ}{Z-Z_0}=\frac{f(Z_0)}{2\pi i}2\pi i=f(Z_0)$

卷积 Convolution

$\int_{-\infty}^\infty f(t)g(x-t)dt=f*g$

t：哑指标，$t+(x-t)=x$

常见性质

线性
交互律
- $f\star g=g\star f$
结合律
- $(f\star g)\star k=f\star (g\star k)$

运用

有 $u(x,y)=f(x)·g(y)$, 期望求关于 $s=x+y$ 的概率密度, 就是 $f*g$

傅里叶展开

傅里叶级数：表示$2\pi$为周期

$f(x)=\frac{1}{2}a_0+\sum_{n=1}^\infty a_nCosnx+\sum_{n=1}^\infty b_nSinnx$

以 $\{\mathbb{I},Sinnx,Cosnx\}$ 为基向量

其中

$\frac{1}{2\pi}\int_0^{2\pi}SinnxSinmx\ dx=\begin{cases}0&m\ne n\\\frac{1}{2}&m=n\ne 0\\0&m=n=0\end{cases}$ $\frac{1}{2\pi}\int_0^{2\pi}CosnxCosmx\ dx=\begin{cases}0&m\ne n\\\frac{1}{2}&m=n\ne 0\\1&m=n=0\end{cases}$ $\int_0^{2\pi}SinnxCosmx\ dx=0$

可证得正交性被满足

$\int_0^{2\pi}f(x)Cosnx\ dx=\int_0^{2\pi}a_nCosnxCosnx\ dx=\pi a_n$ $a_n=\frac{1}{\pi}\int_0^{2\pi}f(x)Cosnx\ dx$

同理

$b_n=\frac{1}{\pi}\int_0^{2\pi}f(x)Sinnx\ dx$

and

$a_0=\frac{1}{\pi}\int_0^{2\pi}f(x)\ dx=2$

使得常值为 1

【Example 1】

$a_0=\frac{1}{\pi}\int_0^\pi f(x)dx=1$

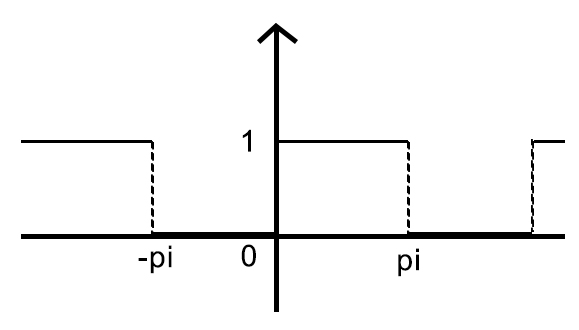
$a_0$ 通常是均值

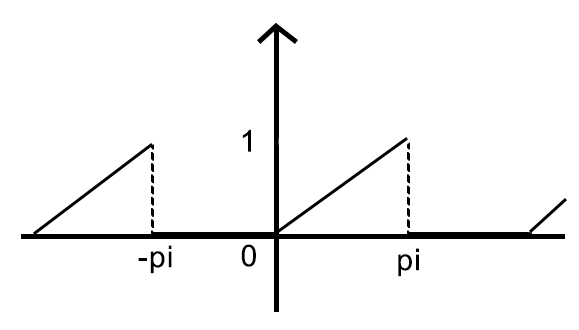
$\begin{align} a_n&=\frac{1}{\pi}\int_0^\pi f(x)Cosnx\ dx\\ &=\frac{1}{\pi}\int_0^\pi Cosnx\ dx\\ &=\frac{1}{n\pi}\int_0^\pi Cosnx\ dnx\\ &=\frac{1}{n\pi}\int_0^\pi dSinnx\\ &=\frac{1}{n\pi} Sinnx|_0^\pi=0-0 \end{align}$ $\begin{align} b_n&=\frac{1}{\pi}\int_0^\pi f(x)Sinnx\ dx\\ &=\frac{1}{\pi}\int_0^\pi Sinnx\ dx\\ &=\frac{1}{n\pi}\int_0^\pi Sinnx\ dnx\\ &=\frac{1}{n\pi}\int_0^\pi -\ dCosnx\\ &=-\frac{1}{n\pi} Cosnx|_0^\pi\\ &=\begin{cases}\frac{2}{n\pi}& n=2k+1\\ 0&n=2k \end{cases} \end{align}$ $f(x)=\frac{1}{2}+\frac{2}{\pi}(Sinx+\frac{Sin3x}{3}+\frac{Sin5x}{5}+...)$

当 $Sinnx$ 项加的越多 $n\to\infty$, 越趋近目标图像. 但当不够多时，振动会比较剧烈，且存在吉布斯现象/音爆 (可用小波变换解决)

如果将原目标往左移 $\frac{\pi}{2}$ , $x\to x+\frac{\pi}{2}$

$Sinx$ 向左移 $\frac{\pi}{2}$ 得到 $Cosx$, $Cosx$ 向左移 $\frac{\pi}{2}$ 得到 $-Sinx$

$Sinx$ 向右移 $\frac{\pi}{2}$ 得到 $-Cosx$, $Cosx$ 向右移 $\frac{\pi}{2}$ 得到 $Sinx$

$\begin{align} f(x+\frac{1}{2}\pi)&=\frac{1}{2}+\frac{2}{\pi}(Sin(x+\frac{1}{2}\pi)+\frac{Sin(3x+\frac{3}{2}\pi)}{3}+\frac{Sin(5x+\frac{5}{2}\pi)}{5}+...)\\ &=\frac{1}{2}+\frac{2}{\pi}(Cosx-\frac{Cos3x}{3}+\frac{Cos5x}{5}-...) \end{align}$

令 $x=0$

$1=\frac{1}{2}+\frac{2}{\pi}(1-\frac{1}{3}+\frac{1}{5}-...)$

得出一个重要的恒等式

$\frac{\pi}{4}=1-\frac{1}{3}+\frac{1}{5}-...$

【Example 2】

$a_0=\frac{1}{\pi}\frac{x^2}{2}|_0^\pi=\frac{\pi}{2}$

$\int udv=uv-\int vdu$

$\begin{align} a_n&=\frac{1}{n\pi}\int_0^\pi x\ dSinnx\\ &=\frac{1}{n\pi}[0-\int_0^\pi Sinnx\ dx]\\ &=\frac{1}{n^2\pi}Cosnx|_0^\pi\\ &=\begin{cases}-\frac{2}{n^2\pi}&n=2k+1\\0&n=2k\end{cases} \end{align}$ $\begin{align} b_n&=\frac{1}{n\pi}\int_0^\pi -x\ dCosnx\\ &=\frac{1}{n\pi}[\int_0^\pi Cosnx\ dx+\pi]\\ &=\frac{1}{n^2\pi}Sinnx|_0^\pi-\frac{Cosn\pi}{n}\\ &=\frac{(-1)^{n-1}}{n} \end{align}$ $f(x)=\frac{\pi}{4}-\frac{2}{\pi}(Cosx+\frac{Cos3x}{3^2}+\frac{Cos5x}{5^2}+...)+(Sinx-\frac{Sin2x}{2}+\frac{Sin3x}{3}-...)$

令 $x=0$

$0=\frac{\pi}{4}-\frac{2}{\pi}(1+\frac{1}{3^2}+\frac{1}{5^2}+...)$

得出一个重要的恒等式

$\frac{\pi^2}{8}=1+\frac{1}{3^2}+\frac{1}{5^2}+...$

扩充到复数域

以复数与共轭替换原表达式

$\begin{align} f(x)&=\frac{a_0}{2}+\sum_{n=1}^\infty a_nCosnx+\sum_{n=1}^\infty b_nSinnx\\ &=\frac{a_0}{2}+\sum_{n=1}^\infty a_n(\frac{e^{inx}+e^{-inx}}{2})+\sum_{n=1}^\infty b_n(\frac{e^{inx}-e^{-inx}}{2i})\\ &\Rightarrow c_n\sum_{n=-\infty}^\infty e^{inx} \end{align}$

此时

当 $n>0$

$c_n=\frac{a_n}{2}-\frac{ib_n}{2}$

当 $n<0$

$c_{-n}=\frac{a_{-n}}{2}+\frac{ib_{-n}}{2}$

当 $n=0$

$f(x)=\frac{a_0}{2}+振动=c_0+振动$

以 $e^{inx}$ 为基向量

$\begin{align} &\int_0^{2\pi}e^{inx}·e^{-imx}dx\\ =&\int_0^{2\pi}e^{i(n-m)x}dx\\ =&\int_0^{2\pi}Cos(n-m)x+iSin(n-m)x\ dx\\ =&\begin{cases}2\pi&m=n\\0&m\ne n\end{cases} \end{align}$

可证得正交性被满足

$c_n=\frac{1}{2\pi}\int_0^{2\pi}f(x)·e^{-inx}dx$

帕塞瓦尔定理

$E(f^2(x))=\frac{1}{2\pi}\int_0^{2\pi}f^2(x)dx=(\frac{a_0}{2})^2+\sum_{n=1}^\infty(\frac{1}{2}a_n^2+\frac{1}{2}b_n^2)$ $E(f^2(x))=\frac{1}{2\pi}\int_0^{2\pi}|f(x)|^2dx=\sum_{n=1}^\infty|c_n|^2,\ \frac{a_0}{2}=c_0$

where $|f(x)|^2=f(x)\bar{f}(x)$

傅里叶变换

将原先以 $(-\pi,\pi)$ 为一周期，改写为以 $(-L,L)$ 为一周期

$Cosnx \Leftrightarrow Cosn(\frac{2\pi x}{2L})=Cos\frac{n\pi x}{L}$ $Sinnx \Leftrightarrow Sin\frac{n\pi x}{L}$ $e^{inx}\Leftrightarrow e^{\frac{in\pi x}{L}}$ $a_n=\frac{1}{\pi}\int_{-\pi}^\pi f(x)Cosnx\ dx\Leftrightarrow \frac{1}{L}\int_{-L}^L f(x)Cos\frac{n\pi x}{L}\ dx$ $c_n\Leftrightarrow\frac{1}{L}\int_{-L}^Lf(x)·e^{-\frac{in\pi x}{L}}dx$

普通 $2L$ 周期的展开

$f(x)=\sum_{n=-\infty}^\infty c_n e^{\frac{in\pi}{L}x}$

定义：$\frac{n\pi}{L}=\alpha_n$, $\Delta \alpha=\alpha_{n+1}-\alpha_n=\frac{\pi}{L}$

$f(x)=\sum_{n=-\infty}^\infty c_n e^{i\alpha_nx}$ $c_n=\frac{1}{2L}\int_{-L}^Lf(x)e^{-i\alpha_nx}dx=\frac{\Delta\alpha}{2\pi}\int_{-L}^Lf(x)e^{-i\alpha_nx}dx$

把 $c_n$ 代入 $f(x)$

$\begin{align} f(x)&=\sum_{n=-\infty}^\infty \frac{\Delta\alpha}{2\pi} \int_{-L}^Lf(u)e^{-i\alpha_nu}du\ e^{i\alpha_nx}\\ &=\frac{1}{2\pi}\sum_{n=-\infty}^\infty \int_{-L}^Lf(u)e^{i\alpha_n(x-u)}du\ \Delta\alpha\\ \end{align}$

令 $L\to\infty$, 有 $\Delta\alpha\to 0$

$f(x)=\frac{1}{2\pi}\int_{-\infty}^\infty\int_{-\infty}^\infty f(u)e^{i\alpha_n(x-u)}du\ d\alpha\\$

可以将上式拆成两份

$f(x)=\frac{1}{2\pi}\int_{-\infty}^\infty g(\alpha)e^{i\alpha_nx}d\alpha\\$ $g(\alpha)=\int_{-\infty}^\infty f(u)e^{-i\alpha_nu}du$

双重可逆定义

$f(x) \leftrightarrow g(\alpha)$

总结得

$F.T\begin{cases} g(\alpha)=\int_{-\infty}^\infty f(x)e^{-i\alpha_nx}dx\\ f(x)=\frac{1}{2\pi}\int_{-\infty}^\infty g(\alpha)e^{i\alpha_nx}d\alpha\\ \end{cases}$

有时候表达式不同，但积分前的数相乘必须等于$\frac{1}{2\pi}$

$\begin{align} f'(x)&\leftrightarrow\int_{-\infty}^\infty f'(x)e^{-i\alpha_nx}dx\\ &=f(x)e^{-i\alpha_nx}|_{-\infty}^\infty-\int_{-\infty}^\infty (-i\alpha_n)f(x)e^{-i\alpha_nx}dx\\ &=0+i\alpha_ng(\alpha) \end{align}$

因此可推导

$f''(x)\leftrightarrow(i\alpha)^2g(\alpha),\ f'''(x)\leftrightarrow(i\alpha)^3g(\alpha)$

此方法可以用来 $求导\leftrightarrow乘积$

$(3f'''(x)+2f''(x)+f(x))\rightarrow多项式$ $f(x)\leftarrow g(\alpha)$

如果采用

$\int_{-\infty}^\infty f(x)e^{-\alpha x}dx$

则是拉普拉斯变换

傅里叶变换的正式表达

$\mathscr{F}(f(x))(\alpha)=g(\alpha)$ $\mathscr{F}(g(\alpha))(x)=f(x)$

帕塞瓦尔定理

函数的模（在一定区间内的积分）= 所有系数的平方和的叠加；能量没有损失

$\int_{-\infty}^\infty|g(\alpha)|^2d\alpha=2\pi\int_{-\infty}^\infty|f(x)|^2dx$

证明

$\begin{align} \int_{-\infty}^\infty|g(\alpha)|^2d\alpha&=\int_{-\infty}^\infty g(\alpha)\bar{g}(\alpha)d\alpha\\ &=\int_{-\infty}^\infty g(\alpha)(\int_{-\infty}^\infty\bar{f}(x)e^{idx}dx)d\alpha\\ &=\int_{-\infty}^\infty \bar{f}(x)(\int_{-\infty}^\infty g(\alpha)e^{idx}d\alpha)dx\\ &=2\pi\int_{-\infty}^\infty \bar{f}(x)f(x)dx \end{align}$

特性

线性性

有 F.T : $f\to g$, $t\to s$

$\mathscr{F}(\alpha f+\beta t)=\alpha g+\beta s$

求导特性

$f^{(n)}(x)\leftrightarrow(i\alpha)^ng(\alpha)$ $(-ix)^nf(x)\leftrightarrow g^{(n)}(\alpha)$

卷积特性

有 F.T : $f\to g$, $t\to s$

$f*t\leftrightarrow g*s$

不确定性关系 Uncertainty Principle

$\Delta X\Delta P\ge\frac{\hbar}{2}$

$G(引力), \hbar (普朗克常量量子), c (时定)$

求正态分布分F.T

$f(x)=\frac{1}{\sqrt{4\pi a}}e^{-\frac{x^2}{4a}}$ $\mathscr{F}(f(x))=e^{-\alpha u^2}$

用到解析函数在解析区域内围道积分=0

$\begin{align} g(u)&=\int_{-\infty}^\infty f(x)e^{-iux}dx\\ &=\frac{1}{\sqrt{4\pi a}}\int_{-\infty}^\infty e^{-\frac{x^2}{4a}}e^{-iux}dx\\ &=\frac{1}{\sqrt{4\pi a}}e^{-au^2}\int_{-\infty}^\infty e^{-(\frac{x^2}{4a}+iux+a(iu)^2)}dx\\ &=\frac{1}{\sqrt{4\pi a}}e^{-au^2}\int_{-\infty}^\infty e^{-(\frac{x}{2\sqrt{a}}+\sqrt{a}iu)^2}dx\\ \end{align}$

Recall

$\int_{-\infty}^\infty e^{-x^2}dx=I=\sqrt{\pi}$

证明

$\begin{align} I^2&=\int_{-\infty}^\infty e^{-x^2}dx\int_{-\infty}^\infty e^{-y^2}dy\\ &=\int\int_{-\infty}^\infty e^{-(x^2+y^2)}dx\ dy\\ &=\int_0^{2\pi}\int_{-\infty}^\infty e^{-r^2}rdr\ d\theta\\ &=\pi\int_{-\infty}^\infty e^{-r^2}dr^2\\ &=\pi \end{align}$

$\int\int_Df(x,y)dxdy=\int\int_Df(\rho Cos\theta,\rho Sin\theta)\rho d\rho d\theta$

$\oint_{I-II}e^{-z^2}dZ=0$ $II:\int_{-\infty}^\infty e^{-(\frac{x}{2\sqrt{a}}+\sqrt{a}iu)^2}dx=I:\int_{-\infty}^\infty e^{-(\frac{x}{2\sqrt{a}})^2}dx=2\sqrt{a}\int_{-\infty}^\infty e^{-x'^2}dx'=2\sqrt{a\pi}$

从另一种角度解释了正态分布的形成

所以

$\begin{align} g(u)&=\frac{1}{\sqrt{4\pi a}}e^{-au^2}·2\sqrt{a\pi}\\ &=e^{-au^2} \end{align}$

引入定理

$\psi(x)=\frac{1}{\sqrt{4\pi a}}e^{-\frac{x^2}{4a}}$ $P(k)=e^{-ak^2}$

with $4a=2\sigma_x^2$, $\frac{1}{a}=2\sigma_k^2$; $\sigma_x\sigma_k=const.$ 位置越确定，动量越不确定，反之亦然. 两者只有一种能优化到一种程度.

解热传导公式

此步骤可以套入由BS-PDE推导的BS model

初始热温分布 $f(x)$, 目标函数 $h(x,t)$ 在 t 时间 x 位置的温度.

热传导方程

$\frac{\partial h(x,t)}{\partial t}=k\frac{\partial^2 h(x,t)}{\partial x^2}$

在 t 时增加的温度，是两边温差的差乘以一个系数

选择 x 消去，用 F.T $x\to u$

$\begin{align} \mathscr{F}(\frac{\partial h}{\partial t})&=\mathscr{F}(k\frac{\partial^2 h}{\partial x^2})\\ \frac{\partial}{\partial t}[\mathscr{F}(h)]&=k(iu)^2\mathscr{F}(h) \end{align}$

因为有 $\frac{d}{dt}W=aW$, 判断 $\mathscr{F}(h)$ 为指数形式

$\mathscr{F}(h)=c(u)e^{-ku^2t}$

由卷积特性，若 F.T : $f\to g$, $t\to s$, 有$f\star t\leftrightarrow g\star s$

因为存在初态 t=0 时，$h(x,0)=f(x)$

$\mathscr{F}(f(x))=c(u)e^{-ku^20}=c(u)$

依照正态分布分F.T得出

$\mathscr{F}(\frac{1}{\sqrt{4\pi kt}}e^{-\frac{x^2}{4kt}})=e^{-ku^2t}$

总结

$h(x,t)=\int_{-\infty}^\infty f(L)\frac{1}{\sqrt{4\pi kt}}e^{-\frac{(x-L)^2}{4kt}}dL$

核磁共振成像 MRI

密度分布 $\mu(x,y)$，原强度 $I_0$，穿透后的强度 $I=I_0e^{-\int_L \mu}$，现已知 $\int_L \mu$, $\theta$ 射入角度，$\rho$ 距圆心距离

将变换扩展到二维

$F.T\begin{cases} g(k_x,k_y)=\int\int f(x,y)e^{-i(k_xx+k_yy)}dxdy\\ f^{(n)}(x,y)\leftrightarrow(i(k_xx+k_yy))^ng(k_x,k_y)\\ \end{cases}$

固定 $\theta$，改变 $\rho$，并对 $\rho$ 进行 F.T

$\begin{align} \mathscr{F}(\int_L \mu(\rho,\theta))(r)&=\int(\int_L \mu(\rho,\theta))e^{-ir\rho}d\rho\\ &=\int\int \mu(x,y)e^{-ir(xCos\theta+ySin\theta)}dxdy\\ \end{align}$

变量替换 $rCos\theta=k_x, rSin\theta=k_y$

$\begin{align} \mathscr{F}(\int_L \mu(\rho,\theta))(r)&=\int\int \mu(x,y)e^{-i(k_xx+k_yy)}dxdy\\ \end{align}$

得到 $\mathscr{F}(\mu(x,y))$ 后，I.F.T，得到 $\mu(x,y)$

离散傅里叶变换

等效与矩阵算法，发展为快速傅里叶变换 F.F.T

定义 [x] 中括号为离散, 以下是 D.F.T, $2\pi$ 为一个周期

$\mathscr{F}(f[n])(m)\equiv\sum_{n=0}^{N-1}f[n]e^{-2\pi inm/N}$

矩阵形式

$W_{nm}=e^{-\frac{2\pi i}{N}nm},\ m,n\in[0,N-1]$ $\mathscr{F}(f[n])(m)= Wf[n]$

定义 $e^{-\frac{2\pi i}{N}}=\omega$

$W=\begin{bmatrix} 1&1&1&...&1\\ 1&\omega&\omega^2&...&\omega^m\\ 1&\omega^{2}&\omega^{4}&...&\omega^{2m}\\ ...&...&...&...&...\\ 1&\omega^{n}&\omega^{2n}&...&\omega^{mn}\\ \end{bmatrix}$ $W^{-1}=\frac{1}{N}\begin{bmatrix} 1&1&1&...&1\\ 1&\omega^{-1}&\omega^{-2}&...&\omega^{-m}\\ 1&\omega^{-2}&\omega^{-4}&...&\omega^{-2m}\\ ...&...&...&...&...\\ 1&\omega^{-n}&\omega^{-2n}&...&\omega^{-mn}\\ \end{bmatrix}$ $WW^{-1}=I$

快速傅里叶变换

有 $e^{i\theta}=Cos\theta+iSin\theta$, 在 $e^{-\frac{2\pi i}{N}nm}$ 中，当 nm 能被 N 整除，则 $W_{mn}$ 等于 1

$W_{N\times N}$ 可以分成 $一个分块矩阵\times一个对角分块矩阵\times位移矩阵$

$W_{N\times N}= \begin{bmatrix} I&D\\I&-D \end{bmatrix} \begin{bmatrix} W_{\frac{N}{2}}&0\\0&W_{\frac{N}{2}} \end{bmatrix} \begin{bmatrix} n\leq\frac{N}{2},第n行2n+1列为1\\n\ge\frac{N}{2},第(n-\frac{N}{2})行2(n-\frac{N}{2})列为1 \end{bmatrix}$

D 是一个包含 $[1,\omega,\omega^2,…,\omega^{\frac{N}{2}-1}]$ 的对角矩阵

Gabor变换/短时傅里叶变换

为了研究一段时间，引入$g(t)$ 时窗因子，只在 0 点附近不为 0，其余快速消减

$G(f(t))(w,u)=\int_{-\infty}^\infty f(t)g(t-u)e^{-iwt}dt$

小波变换 Wavelet Transform

$W(f(t))(a,b)=\int_{-\infty}^\infty f(t)\psi_{a,b}(t)dt$ $f(t)=\frac{1}{C}\int_0^\infty\int_{-\infty}^\infty a^{-2}W_f(a,b)\psi_{a,b}(t)db\ da$ $C=\int_0^\infty\frac{|\mathscr{F}(\psi(t))(\omega)|^2}{\omega}d\omega$ $\psi_{a,b}(t)=\frac{1}{\sqrt{a}}\psi(\frac{t-b}{a})$

$a>0$ 放缩尺度因子
$-\infty<b<\infty$ 平移因子
$\psi(t)$ 基函数

基函数/小波平均值必须为0

墨西哥草帽式

$\psi(t)=\frac{2}{B}\pi^{-\frac{1}{4}}(1-t^2)e^{-\frac{t^2}{2}}$

Morlet 小波

$\psi(t)=e^{-\frac{t^2}{2}}e^{i\omega_0t}$

拉普拉斯变换 Laplace Transform

$F.T\begin{cases} \mathscr{L}(f(t))(p)=F(p)=\int_0^\infty f(t)e^{-pt}dt\\ f'(t)\leftrightarrow pF(p)-f(0)\\ f''(t)\leftrightarrow p(pF(p)-f(0))-f'(0)\\ \end{cases}$