【笔记】Financial_Mathematics

基于 ChiuFai WONG 教授的FM课件进行的零碎知识的整理；

Chapter 1 Annuities

• $i_t=\frac{a(t)-a(t-1)}{a(t-1)}$ , $d_t=\frac{a(t)-a(t-1)}{a(t)}$

• $a(t)=(1+i)^t$ compound interest accumulation function

• $a(t)=(1-d)^{-t}$ compound discount accumulation function

• $1-d=v=\frac1{1+i}$

• $i^{(m)}$ nominal rate of interest compounded m times a year

• $(1+\frac{i^{(m)}}m)^m=1+i$ , $i^{(m)}=m((1+i)^{1/m}-1)$

• $d^{(m)}$ nominal rate of discount compounded m times a year

• $(1-\frac{d^{(m)}}m)^m=1-d$ , $d^{(m)}=m(1-(1-d)^{1/m})$

• $a_{_n\bigg\urcorner_i}=\frac{1-v^{n}}{i}$ annuity-immediate

  

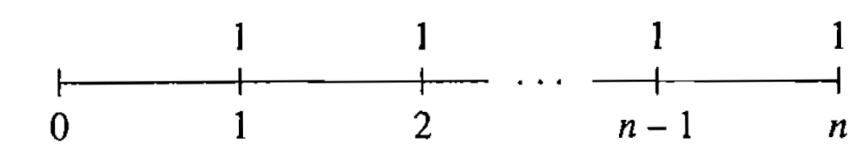
• $S_{_n\bigg\urcorner_i}=(1+i)^na_{_n\bigg\urcorner_i}=\frac{(1+i)^n-1}{i}$

• $\ddot a_{_n\bigg\urcorner_i}=\frac{1-v^{n}}{d}$ annuity-due , $\ddot a_{_n\bigg\urcorner_i}=(1+i)a_{_n\bigg\urcorner_i}=1+a_{_{n-1}\bigg\urcorner_i}$

  

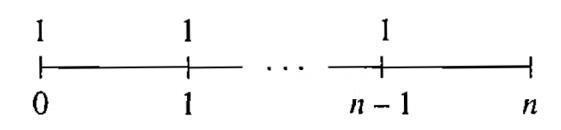
• $\ddot S_{_n\bigg\urcorner_i}=\frac{(1+i)^n-1}{d}$ , $S_{_n\bigg\urcorner_i}=(1+i)^{-1}\ddot S_{_n\bigg\urcorner_i}=1+\ddot S_{_{n-1}\bigg\urcorner_i}$

• $a_{_\infty\bigg\urcorner_i}=\frac{1}{i}$ perpetuity-due

• $\frac{a_{_n\bigg\urcorner_i}}{S_{_k\bigg\urcorner_i}}$ pays 1 at the end of each k interest periods for a total of n interest periods

  

• $\frac{a_{_n\bigg\urcorner_i}}{a_{_k\bigg\urcorner_i}}$ pays 1 at the beginning of each k interest periods for a total of n interest periods

  

• $a_{_n\bigg\urcorner_i}^{(m)}=\frac{1-v^n}{i^{(m)}}$ pays 1/m at the end of each m-th of an interest period for a total of n interest periods

  

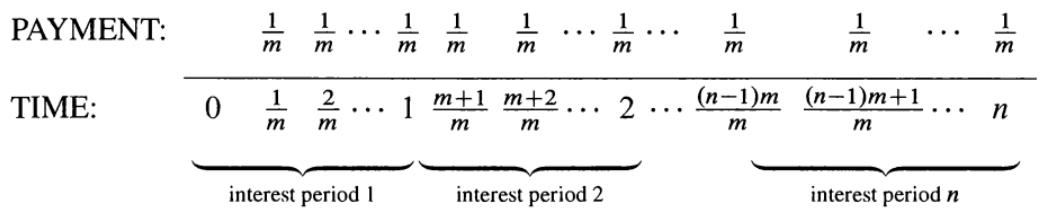
• $S_{_n\bigg\urcorner_i}^{(m)}=\frac{(1+i)^n-1}{i^{(m)}}$

• $\ddot a_{_n\bigg\urcorner_i}^{(m)}=\frac{1-v^n}{d^{(m)}}$ pays 1 m at the end of each m-th of an interest period for a total of n interest periods

  

• $S_{_n\bigg\urcorner_i}^{(m)}=\frac{(1+i)^n-1}{d^{(m)}}$

Chapter 2 Forwards and Futures

$$\begin{array}{|c|c|c|} \hline \text { Underlying asset } & \text { Forward price } F_{t, T} & \text { Prepaid forward price } F_{t, T}^{P} \\ \hline \text { Non-dividend pay stock } & S(t) e^{r(T-t)} & S(t) \\ \hline \text { Discrete dividend paying stock } & S(t) e^{r(T-t)}-\text { CumValue(Divs) } & S(t)-\mathrm{PV}_{t, T}(\text { Divs }) \\ \hline \text { Continuous dividend paying stock } & S(t) e^{(r-\delta)(T-t)} & S(t) e^{-\delta(T-t)} \\ \hline \begin{array}{c} \text { Currency, denominated in currency } \\ d \text { for delivery of currency } f \end{array} & x(t) e^{\left(r_{d}-r_{f}\right)(T-t)} & x(t) e^{-r_{f}(T-t)} \\ \hline \end{array}$$

Chapter 3 Options

• $\Delta=\frac{f_{u}-f_{d}}{S(0) u-S(0) d}$
• $p=\frac{e^{(r-\delta) T}-d}{u-d}$ (on the futures $p=\frac{1-d}{u-d}$)
• $f=e^{-r T}\left(p f_{u}+(1-p) f_{d}\right)$ expected future payoff in a risk-neutral world discounted at the risk-free rate

Cox-Ross-Rubinstein Formula

$$C_{E u r}(S(0), K, N \Delta t)=S(0)\left[1-\Phi\left(m-1, N, p u e^{-r \Delta t}\right)\right]-e^{-r N \Delta t} K[1-\Phi(m-1, N, p)]$$ $$P_{E u r}(S(0), K, N \Delta t)=e^{-r N \Delta t} K \Phi(m-1, N, p)-S(0) \Phi\left(m-1, N, p u e^{-r \Delta t}\right)$$

In order to match the stock price volatility with the tree’s parameters, we must therefore have

$$\begin{aligned} \sigma^{2} \Delta t &=p u^{2}+(1-p) d^{2}-(p u+(1-p) d)^{2} \\ &=p(1-p) u^{2}+p(1-p) d^{2}-2 p(1-p) u d \\ &=p(1-p)(u-d)^{2} \\ &=\left(u-e^{r \Delta t}\right)\left(e^{r \Delta t}-d\right) \\ &=e^{r \Delta t}(u+d)-u d-e^{2 r \Delta t} \end{aligned}$$

where

$$u=e^{\sigma \sqrt{\Delta t}} \quad \text { and } \quad d=e^{-\sigma \sqrt{\Delta t}}$$

Black-Scholes Formula

$$C=S(0) N\left(d_{1}\right)-K e^{-r T} N\left(d_{2}\right) \quad \text { and } \quad P=K e^{-r T} N\left(-d_{2}\right)-S(0) N\left(-d_{1}\right)$$

where

$$d_1=\frac{\ln(S_0/K)+(r + \frac{\sigma^2}{2})T}{\sigma\sqrt T}$$ $$d_2=\frac{\ln(S_0/K)+(r - \frac{\sigma^2}{2})T}{\sigma\sqrt T}=d_1-\sigma\sqrt{T}$$

Put-Call parity

$$C(K,T)-P(K,T)=S(0)-Ke^{-rT}-PV_{0,T}(Divs)$$

For put futures option

$$C(K,T)-P(K,T)=F(0)e^{-rT}-Ke^{-rT}$$

The put-call parity result for currency options (in domestic HK dollars) is

$$C_d(x(0),K,T)-P_d(x(0),K,T)=x(0)e^{-r_fT}-Ke^{-r_dT}$$

$C_d(x(0),K,T)$ purchase 1 foreign currency(US dollars) for K domestic currency

$$\underbrace{C_{d}(x(0), K, T)}_{\text {domestic curency }}=\underbrace{Kx(0) P_{f}\left(\frac{1}{x(0)}, \frac{1}{K}, T\right)}_{\text {foreign curency }}$$

Exchange option

$$C(S_1(t),S_2(t),T-t)-P(S_1(t),S_2(t),T-t)=F_{t,T}^P(S_1)-F_{t,T}^P(S_2)$$

or

$$C(S_1(t),S_2(t),T-t)-C(S_2(t),S_1(t),T-t)=F_{t,T}^P(S_1)-F_{t,T}^P(S_2)$$ $$P(S_2(t),S_1(t),T-t)-P(S_1(t),S_2(t),T-t)=F_{t,T}^P(S_1)-F_{t,T}^P(S_2)$$

Early exercise of American call option

$$\begin{aligned} C_{A m e r}(S(t), K, T-t) & \geq C_{E u r}(S(t), K, T-t) \\ &=P_{E u r}(S(t), K, T-t)+F_{t, T}^{P}(S)-K e^{-r(T-t)} \\ &=P_{E u r}(S(t), K, T-t)+S(t)-\mathrm{PV}_{t, T}(\mathrm{Div})-K e^{-r(T-t)} \\ &=P_{E u r}(S(t), K, T-t)+\underbrace{(S(t)-K)}_{\text {call exercise value at } t}+\underbrace{K\left(1-e^{-r(T-t)}\right)}_{\text {PV of interest of } K \text { in } T-t}-\mathrm{PV}_{t, T}(\text { Div) } \end{aligned}$$

The put option must be worth at least 0. Early exercise will not be rational if $PV_{t,T}(Div)<K(1-e^{-r(T-t)})$ , because $C_{Amer}\ge(S(t)-K)$

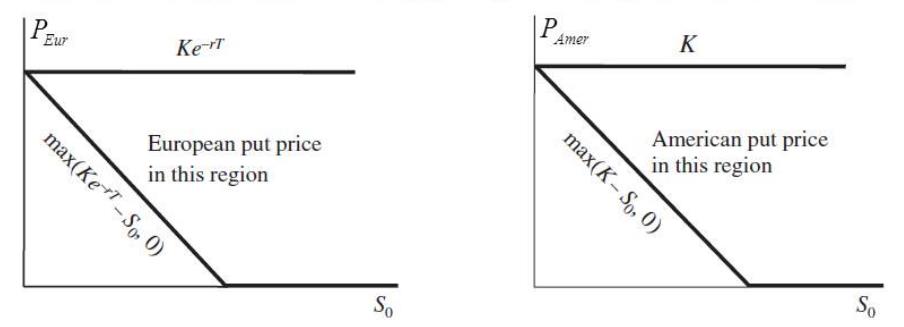
The bounds for European and American put option on a non-dividend-paying stock

Chapter 4 Black-Scholes Equations

Let $X_i$, either $\sqrt{t/n}$ or $-\sqrt{t/n}$, $Z_n=\sum_{i=1}^nX_i$

The quadratic variation of the random walk is defined by

$$\sum_{i=1}^n(Z_i-Z_{i-1})^2=\sum_{i=1}^nX_i^2=t$$

If the time steps go to zero , $Z(t)$ is called Brownian motion

$$(dZ(t))^2=dt,\quad dZ(t)\sim N(0,dt)$$

Let $S(t)$ be stock price at time t

$$dS(t)=\alpha S(t)dt+\sigma S(t)dZ(t)$$ $$S(t)=S(0)e^{\sigma Z(t)+(\alpha -\frac12 \sigma^2)t}$$

Let us analyze a portfolio $W$

$$W(t)=\varphi S(t)+(1-\varphi)B(t)$$

Hence

$$\frac{d W(t)}{W(t)}=(\varphi \alpha+(1-\varphi) r) d t+\varphi \sigma d Z(t)$$ $$\frac{W(t)}{W(0)}=e^{(\varphi \alpha+(1-\varphi) r-0.5\varphi^2\sigma^2)t+\varphi \sigma d Z(t)}=\left(\frac{S(t)}{S(0)}\right)^{\varphi}e^{(1-\varphi)(r+0.5\varphi\sigma^2)t}$$

with $\delta_s$ and $\delta_w$ be the continuous dividend rates of the stock and the portfolio

$$\frac{W(t)}{W(0)}=\left(\frac{S(t)}{S(0)}\right)^{\varphi}e^{(\varphi\delta_s-\delta_w+(1-\varphi)r-0.5\varphi^2\sigma^2+0.5\phi\sigma^2)t}$$

Sharpe ratio

If $c_1S_1(t)+c_2S_2(t)$ is a risk free portfolio with risk-free interest rate $r$

$$c_{1}\left(\alpha_{1}-\delta_{1}\right) S_{1}(t)+c_{2}\left(\alpha_{2}-\delta_{2}\right) S_{2}(t)=r\left(c_{1} S_{1}(t)+c_{2} S_{2}(t)\right)$$

with $c_1\sigma_1S_1(t)\pm c_2\sigma_2S_2(t)=0$

$$\frac{\alpha_{1}-\delta_{1}-r}{\sigma_{1}}=\pm \frac{\alpha_{2}-\delta_{2}-r}{\sigma_{2}}$$

Black-Scholes for currency

$$C=x(t)e^{-r_f T}N\left(d_{1}\right)-K e^{-r T} N\left(d_{2}\right) \quad \text { and } \quad P=K e^{-r T} N\left(-d_{2}\right)-x(t)e^{-r_f T}N\left(-d_{1}\right)$$

Black-Scholes for options on Future

$$C=Fe^{-r T}N\left(d_{1}\right)-K e^{-r T} N\left(d_{2}\right) \quad \text { and } \quad P=K e^{-r T} N\left(-d_{2}\right)-Fe^{-r T}N\left(-d_{1}\right)$$

Black-Scholes PDE for options on Future

$$\frac{\partial V}{\partial t}+\frac{1}{2} \sigma^{2} F^{2} \frac{\partial^{2} V}{\partial F^{2}}-r V=0$$

Chapter 5 Greek Symbol and Hedging

Black-Scholes partial differential equation

$$\frac{\partial V}{\partial t}+\frac{1}{2} \sigma^{2} S^{2} \frac{\partial^{2} V}{\partial S^{2}}+(r-\delta) S \frac{\partial V}{\partial S}-r V=0$$

gives us the relation between Greek symbols

$$\theta+(r-\delta) \Delta S+0.5 S^{2} \sigma^{2} \Gamma=r V$$

A better approximation of the change on option value

$$f(x)=f(x_0)+f'(x_0)(x-x_0)+\frac12f''(x_0)(x-x_0)^2+error$$

set $\varepsilon=S(t+h)-S(t)$ , $x_0=S(t)$ , $x=S(t+h)$ , $f(x_0)=V(S(t))$ , $f’(x_0)=\Delta$ , $f’’(x_0)=\Gamma$ , error term $=\theta h$

$$V(S(t+h))=V(S(t))+\Delta \varepsilon+\frac{1}{2} \Gamma \varepsilon^{2}+\theta h$$

Consider a delta-neutral portfolio

$$V(S(t+h))-V(S(t))=\frac{1}{2} \Gamma \varepsilon^{2}+\theta h$$

The market-maker makes

Assume a delta hedged portfolio consists of selling (or buying) an option $V(0)$, buying $\Delta$ shares of stock $S(0)$, and borrowing the money needed for the other two transactions $\Delta S(0)-V(0)$.

$$Profit = -\overbrace{(V(h)-V(0))}^{\text{change in the value of the option}}+\Delta\overbrace{(S(h)-S(0))}^{\text{change in the price of the stock}}-\overbrace{(e^{rh}-1)(\Delta S(0)-V(0))}^{\text{Interest on the borrowed money}}+\overbrace{\delta h\Delta S(0)}^{\text{dividend}}$$

If we approximate $e^{rh}-1$ as $rh$

$$\begin{aligned} \text { Profit }&=-(V(h)-V(0))+\Delta(S(h)-S(0))-\left(e^{r h}-1\right)(\Delta S(0)-V(0))+\delta h\Delta S(0)\\ &\approx-\left(\overbrace{\frac{1}{2} \Gamma \varepsilon^{2}}^{\text{change of stock price effect}}+\overbrace{\theta h}^{\text{time decay of option}}+\overbrace{rh(\Delta S(0)-V(0))}^{\text{interest effect}}-\delta h\Delta S(0)\right) \quad\text{[by delta-gamma-theta approximation]}\\ &=-\left(\frac{1}{2} \Gamma \varepsilon^{2}-\frac{1}{2} \Gamma \sigma^{2} S(0)^{2} h\right) \quad \text { [by Black-Scholes Equation] } \end{aligned}$$