【笔记】高等数学复习笔记-线性代数

基于 ChiuFai WONG 教授的线性代数课件的笔记；

斯坦福大学CS 229机器学习课程的 基础材料；

与 Coursera 中的 Mathematics for Machine Learning: Linear Algebra 课程 ；

三方教程结合进行整理；

对于部分基础多有忽略，主要用于知识点查找；

1. 基础概念和符号

我们使用以下符号：

• $A \in \mathbb{R}^{m \times n}$，表示 $A$ 为由实数组成具有$m$行和$n$列的矩阵。

• $x \in \mathbb{R}^{ n}$，表示具有$n$个元素的向量。 通常，向量$x$将表示列向量。

  $$x=\left[\begin{array}{c}{x_{1}} \\ {x_{2}} \\ {\vdots} \\ {x_{n}}\end{array}\right]$$

2. 矩阵的运算

2.1 矩阵乘法

• 矩阵乘法结合律: $(AB)C = A(BC)$
• 矩阵乘法分配律: $A(B + C) = AB + AC$
• 矩阵乘法通常不是可交换的; 也就是说，通常$AB \ne BA$。

2.2 Dot Products and Cross Products

详细见连接

3. 矩阵的属性

3.1 单位矩阵和对角矩阵

单位矩阵,$I \in \mathbb{R}^{n \times n} $

$$I_{i j}=\left\{\begin{array}{ll}{1} & {i=j} \\ {0} & {i \neq j}\end{array}\right.$$

对角矩阵,$D= diag(d_1, d_2, . . . , d_n)$

$$D_{i j}=\left\{\begin{array}{ll}{d_{i}} & {i=j} \\ {0} & {i \neq j}\end{array}\right.$$

$ I = diag(1, 1, . . . , 1)$

3.2 转置

$$(A^T)_{ij} = A_{ji}$$

3.3 对称矩阵

如果$A = A^T$，则矩阵$A \in \mathbb{R}^ {n \times n}$是对称矩阵。 如果$ A = - A^T$，它是反对称的。

对于任何矩阵$A \in \mathbb{R}^ {n \times n}$，矩阵$A + A^ T$是对称的，矩阵$A -A^T$是反对称的。 由此得出，任何方矩阵$A \in \mathbb{R}^ {n \times n}$可以表示为对称矩阵和反对称矩阵的和，所以：

$$A=\frac{1}{2}(A+A^T)+\frac{1}{2}(A-A^T)$$

3.4 矩阵的迹

$$\operatorname{tr} A=\sum_{i=1}^{n} A_{i i}$$

对于矩阵 $A$, $B$, $C$, $ABC$为方阵, 则：

• $\operatorname{tr}A =\operatorname{tr}A^T$

• $\operatorname{tr}(A + B) = \operatorname{tr}A + \operatorname{tr}B$ with $A,B \in \mathbb{R}^ {n \times n}$

• $\operatorname{tr}(tA) = t\operatorname{tr}A$ with $ t \in \mathbb{R}$

• $\operatorname{tr}AB = \operatorname{tr}BA$

• $\operatorname{tr}ABC = \operatorname{tr}BCA=\operatorname{tr}CAB$

3.5 范数

欧几里德（$\ell_{2}$）范数，

$$\|x\|_{2}=\sqrt{x^{T} x}=\sqrt{\sum_{i=1}^{n} x_{i}^{2}}$$

$\ell_1$范数:

$$\|x\|_{1}=\sum_{i=1}^{n}\left|x_{i}\right|$$

$\ell_{\infty }$范数：

$$\|x\|_{\infty}=\max _{i}\left|x_{i}\right|$$

以上所提出的三个范数都是$\ell_p$范数族的例子，它们由实数$p \geq 1$参数化，并定义为：

$$\|x\|_{p}=\left(\sum_{i=1}^{n}\left|x_{i}\right|^{p}\right)^{1 / p}$$

Frobenius范数:

$$\|A\|_{F}=\sqrt{\sum_{i=1}^{m} \sum_{j=1}^{n} A_{i j}^{2}}=\sqrt{\operatorname{tr}\left(A^{T} A\right)}$$

范数满足的4个属性（$f : \mathbb{R}^{n} \rightarrow \mathbb{R}$）：

1. 对于所有的 $x \in \mathbb{R}^ {n}$, $f(x) \geq 0 $ (非负).
2. 当且仅当$x = 0$ 时，$f(x) = 0$ (明确性).
3. 对于所有$x \in \mathbb{R}^ {n}$,$t\in \mathbb{R}$，则 $f(tx) = \left| t \right|f(x)$ (正齐次性).
4. 对于所有 $x,y \in \mathbb{R}^ {n}$, $f(x + y) \leq f(x) + f(y)$ (三角不等式)

3.6 线性相关性和秩

矩阵$A \in \mathbb{R}^{m \times n}$的列秩是构成线性无关集合的$A$的最大列子集的大小。行秩是构成线性无关集合的$A$的最大行数。 对于任何矩阵$A \in \mathbb{R}^{m \times n}$，事实证明$A$的列秩等于$A$的行秩，因此两个量统称为$A$的秩，用 $\text{rank}(A)$表示。

• 对于 $A \in \mathbb{R}^{m \times n}$，$\text{rank}(A) \leq min(m, n)$，如果$ \text{rank}(A) = \text{min} (m, n)$，则： $A$ 被称作满秩。
• 对于 $A \in \mathbb{R}^{m \times n}$， $\text{rank}(A) = \text{rank}(A^T)$
• 对于 $A \in \mathbb{R}^{m \times n}$， $B \in \mathbb{R}^{n \times p}$ ， $\text{rank}(AB) \leq \text{min} ( \text{rank}(A), \text{rank}(B))$
• 对于 $A,B \in \mathbb{R}^{m \times n}$， $\text{rank}(A + B) \leq \text{rank}(A) + \text{rank}(B)$

3.7 方阵的逆

方阵$A \in \mathbb{R}^{n \times n}$的倒数表示为$A^{-1}$。但并非所有矩阵都具有逆。如果矩阵的逆存在，则称它为正则/可逆/非奇异，否则称为奇异/不可逆。当矩阵逆存在时，这个逆是唯一的。

If $A_{i j}$ denotes the cofactor of $a_{i j}$, then

$$\begin{aligned} A(\text{adj}(A))&=\left(\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 n} \\ a_{21} & a_{22} & \cdots & a_{2 n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n 1} & a_{n 2} & \cdots & a_{n n} \end{array}\right)\left(\begin{array}{cccc} A_{11} & A_{21} & \cdots & A_{n 1} \\ A_{12} & A_{22} & \cdots & A_{n 2} \\ \vdots & \vdots & \ddots & \vdots \\ A_{1 n} & A_{2 n} & \cdots & A_{n n} \end{array}\right)\\ &=\left(\begin{array}{cccc} A_{11} & A_{21} & \cdots & A_{n 1} \\ A_{12} & A_{22} & \cdots & A_{n 2} \\ \vdots & \vdots & \ddots & \vdots \\ A_{1 n} & A_{2 n} & \cdots & A_{n n} \end{array}\right)\left(\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 n} \\ a_{21} & a_{22} & \cdots & a_{2 n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n 1} & a_{n 2} & \cdots & a_{n n} \end{array}\right) \\ &=\left(\begin{array}{cccc} \text{det}(A) & 0 & \cdots & 0 \\ 0 & \text{det}(A) & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ 0 & \cdots & 0 & \text{det}(A) \end{array}\right)=\text{det}(A) I_{n} \end{aligned}$$

So $A^{-1}=\frac1{\text{det}(A) }\text{adj}(A)$.

3.8 正交阵

如果一个方阵$U\in \mathbb{R}^{n \times n}$的所有列彼此正交并被归一化，则方阵$U$是正交阵。

• $x^Ty=0$，则两个向量$x,y\in \mathbb{R}^{n}$ 是正交

• $|x|_2=1$，则向量$x\in \mathbb{R}^{n}$ 被归一化

• 可以从正交性和正态性的定义中得出，正交矩阵的逆是其转置。

  $$U^ TU = I = U U^T$$

• 在具有正交矩阵的向量上操作不会改变其欧几里德范数，即:

  $$\|U x\|_{2}=\|x\|_{2}$$

注意，如果$U$不是方阵 :即，$U\in \mathbb{R}^{m \times n}$，$n <m$ ，但其列仍然是正交的，则$U^TU = I$，但是$UU^T \neq I$。

3.9 矩阵的值域和零空间

矩阵$A\in \mathbb{R}^{m \times n}$的值域，表示为$\mathcal{R}(A)$

$$\mathcal{R}(A)=\left\{v \in \mathbb{R}^{m} : v=A x, x \in \mathbb{R}^{n}\right\}$$

矩阵$A\in \mathbb{R}^{m \times n}$的零空间 $\mathcal{N}(A)$ 是所有乘以$A$时等于0向量的集合，即：

$$\mathcal{N}(A)=\left\{x \in \mathbb{R}^{n} : A x=0\right\}$$

我们将投影表示为$\operatorname{Proj}\left(y ;\left\{x_{1}, \ldots x_{n}\right\}\right)$，并且可以将其正式定义为:

$$\operatorname{Proj}\left(y ;\left\{x_{1}, \ldots x_{n}\right\}\right)=\operatorname{argmin}_{v \in \operatorname{span}\left(\left\{x_{1}, \ldots, x_{n}\right\}\right)}\|y-v\|_{2}$$

其中$\{x_{1}, \ldots x_{n}\}$的线性组合的所有向量的集合为：

$$\operatorname{span}\left(\left\{x_{1}, \ldots x_{n}\right\}\right)=\left\{v : v=\sum_{i=1}^{n} \alpha_{i} x_{i}, \quad \alpha_{i} \in \mathbb{R}\right\}$$

如果$A$是满秩且$n <m$，向量$y \in \mathbb{R}^{m}$到$A$的范围的投影由下式给出:

$$\operatorname{Proj}(y ; A)=\operatorname{argmin}_{v \in \mathcal{R}(A)}\|v-y\|_{2}=A\left(A^{T} A\right)^{-1} A^{T} y$$

Proof：

$$\begin{aligned}\|A x-y\|_{2}^{2} &=(A x-y)^{T}(A x-y) \\ &=x^{T} A^{T} A x-2 y^{T} A x+y^{T} y \end{aligned}$$ $$\begin{aligned} \nabla_{x}\left(x^{T} A^{T} A x-2 y^{T} A x+y^{T} y\right) &=\nabla_{x} x^{T} A^{T} A x-\nabla_{x} 2 y^{T} A x+\nabla_{x} y^{T} y \\ &=2 A^{T} A x-2 A^{T} y \end{aligned}$$

将最后一个表达式设置为零，然后解出$x$，得到了正规方程：

$$x = (A^TA)^{-1}A^Ty ,\qquad v = A(A^TA)^{-1}A^Ty$$

$\mathcal{R}(A^T)$和 $\mathcal{N}(A)$ 是不相交的子集，它们一起跨越$\mathbb{R}^{n}$的整个空间。 这种类型的集合称为正交补，我们用$\mathcal{R}(A^T)= \mathcal{N}(A)^{\perp}$表示。

$$\left\{w : w=u+v, u \in \mathcal{R}\left(A^{T}\right), v \in \mathcal{N}(A)\right\}=\mathbb{R}^{n} \text { and } \mathcal{R}\left(A^{T}\right) \cap \mathcal{N}(A)=\{\mathbf{0}\}$$

Schmidt 正交化

若$\alpha_{1},\alpha_{2},\cdots,\alpha_{s}$线性无关，则可构造$\beta_{1},\beta_{2},\cdots,\beta_{s}$使其两两正交，且$\beta_{i}$仅是$\alpha_{1},\alpha_{2},\cdots,\alpha_{i}$的线性组合$(i= 1,2,\cdots,n)$，再把$\beta_{i}$单位化，记$\gamma_{i} =\frac{\beta_{i}}{|\beta_{i}|}$，则$\gamma_{1},\gamma_{2},\cdots,\gamma_{i}$是规范正交向量组。其中:

$$\begin{aligned} &\beta_{1} = \alpha_{1},\quad\beta_{2} = \alpha_{2} -\frac{\alpha_{2}·\beta_{1}}{\|\beta_{1}\|^2}\beta_{1},\quad\beta_{3} =\alpha_{3} - \frac{\alpha_{3}·\beta_{1}}{\|\beta_{1}\|^2}\beta_{1} -\frac{\alpha_{3}·\beta_{2}}{\|\beta_{2}\|^2}\beta_{2},\\ &\cdots\\ &\beta_{s} = \alpha_{s} - \frac{\alpha_{s}·\beta_{1}}{\|\beta_{1}\|^2}\beta_{1} - \frac{\alpha_{s}·\beta_{2}}{\|\beta_{2}\|^2}\beta_{2} - \cdots - \frac{\alpha_{s}·\beta_{s - 1}}{\|\beta_{s-1}\|^2}\beta_{s - 1} \end{aligned}$$

3.10 行列式

一个方阵$A \in \mathbb{R}^{n \times n}$的行列式是函数$\text {det}$：$\mathbb{R}^{n \times n} \rightarrow \mathbb{R}^{n} $，并且表示为$\left| A \right|$， 或者$\text{det} A$。$A$的行列式的绝对值是对集合$S$的“体积”的度量。

行列式满足以下属性

$$\left|\left[\begin{array}{ccc}{-} & {t a_{1}^{T}} & {-} \\ {-} & {a_{2}^{T}} & {-} \\ {} & {\vdots} & {} \\ {} & {a_{m}^{T}} & {-}\end{array}\right]\right|=t|A|,\qquad \left|\left[\begin{array}{ccc}{-} & {a_{2}^{T}} & {-} \\ {-} & {a_{1}^{T}} & {-} \\ {} & {\vdots} & {} \\ {-} & {a_{m}^{T}} & {-}\end{array}\right]\right|=-|A|$$ $$\left|\left[\begin{array}{ccc}{-} & {a_{1}^{T}+b_{1}^{T}} & {-} \\ {-} & {a_{2}^{T}} & {-} \\ {} & {\vdots} & {} \\ {} & {a_{m}^{T}} & {-}\end{array}\right]\right|=|A|+\left|\left[\begin{array}{ccc}{-} & {b_{1}^{T}} & {-} \\ {-} & {a_{2}^{T}} & {-} \\ {} & {\vdots} & {} \\ {} & {a_{m}^{T}} & {-}\end{array}\right]\right|$$

对于 $A,B \in \mathbb{R}^{n \times n}$:

• $\left| A \right| = \left| A^T \right|$
• $\left| {AB} \right| = \left| A \right|\left| B \right| = \left| B \right|\left| A \right| = \left| {BA} \right|$，但$\left| A \pm B \right| = \left| A \right| \pm \left| B \right|$不一定成立。
• 有且只有当$A$是奇异时，$\left| A \right|= 0$
• $A$为非奇异时，$\left| A ^{−1}\right| = 1/\left| A \right|$
• $\left| {kA} \right| = k^{n}\left| A \right|$
• $\left| \begin{matrix} & {A\quad O} \ & {O\quad B} \ \end{matrix} \right| = \left| \begin{matrix} & {A\quad C} \ & {O\quad B} \ \end{matrix} \right| = \left| \begin{matrix} & {A\quad O} \ & {C\quad B} \ \end{matrix} \right| =| A||B|$
  ，$A,B$为方阵，$\left| \begin{matrix} {O} & A_{m \times m} \ B_{n \times n} & { O} \ \end{matrix} \right| = ({- 1)}^|A||B|$
• $\lambda_{i}(i = 1,2\cdots,n)$是$A$的$n$个特征值，则$|A| = \prod_{i = 1}^{n}\lambda_{i}$

• Let $\left(\begin{array}{cc}A_{k \times k} & B_{k \times k} \ C_{k \times k} & D_{k \times k}\end{array}\right)$ be a $2 k \times 2 k$ block matrix. Suppose $C_{k \times k} D_{k \times k}=D_{k \times k} C_{k \times k}$ and $\text{det} D_{k \times k} \neq 0$ . Then

  $$\text{det}\left(\begin{array}{cc}A_{k \times k} & B_{k \times k} \\ C_{k \times k} & D_{k \times k}\end{array}\right) =\text{det}\left(A_{k \times k} D_{k \times k}-B_{k \times k} C_{k \times k}\right)$$

范德蒙行列式

$$D_{n} = \begin{vmatrix} 1 & 1 & \ldots & 1 \\ x_{1} & x_{2} & \ldots & x_{n} \\ \ldots & \ldots & \ldots & \ldots \\ x_{1}^{n - 1} & x_{2}^{n 1} & \ldots & x_{n}^{n - 1} \\ \end{vmatrix} = \prod_{1 \leq j < i \leq n}^{}\,(x_{i} - x_{j})$$

克莱姆法则 Cramer’s Rule

Let A be an $n \times n$ nonsingular matrix, and let $\boldsymbol{b} \in \mathbb{R}^{n}$ . Let $A_{i}$ be the matrix obtained by replacing the

i-th column of A by $\boldsymbol{b}$ . If $ \boldsymbol{x}$ is the unique solution of A $\boldsymbol{x}=\boldsymbol{b}$, then

$$x_{i}=\frac{\text{det}\left(A_{i}\right)}{\text{det}(A)} \quad \text { for } i=1, \cdots, n$$

【有趣的例题】

1.

$$\begin{aligned} \left|\begin{array}{ccc}1 & 1 & 1 \\ a & b & c \\ a^{2} & b^{2} & c^{2}\end{array}\right|&=\left|\begin{array}{ccc}1 & 0 & 0 \\ a & b-a & c-a \\ a^{2} & b^{2}-a^{2} & c^{2}-a^{2}\end{array}\right| \quad\left[C_{2}-C_{1} \rightarrow C_{2}, C_{3}-C_{1} \rightarrow C_{3}\right]\\ &=\left|\begin{array}{cc}b-a & c-a \\ b^{2}-a^{2} & c^{2}-a^{2}\end{array}\right|\\ &=(b-a)(c-a)\left|\begin{array}{cc}1 & 1 \\ b+a & c+a\end{array}\right|\\ &=(b-a)(c-a)(c-b) \end{aligned}$$

2.

$$\begin{aligned} \left|\begin{array}{ccc}a+b & b+c & c+a \\ a^{2}+b^{2} & b^{2}+c^{2} & c^{2}+a^{2} \\ a^{3}+b^{3} & b^{3}+c^{3} & c^{3}+a^{3}\end{array}\right|&=\left|\begin{array}{ccc}a & b & c \\ a^{2} & b^{2} & c^{2} \\ a^{3} & b^{3} & c^{3}\end{array}\right|\left|\begin{array}{ccc}1 & 0 & 1 \\ 1 & 1 & 0 \\ 0 & 1 & 1\end{array}\right|\\ &=2abc\left|\begin{array}{ccc}1 & 1 & 1 \\a & b & c \\a^{2} & b^{2} & c^{2} \end{array}\right| \\ &=2 a b c(b-a)(c-a)(c-b) \end{aligned}$$

3.11 二次型和半正定矩阵

给定方矩阵$A \in \mathbb{R}^{n \times n}$和向量$x \in \mathbb{R}^{n}$，标量值$x^T Ax$被称为二次型。

$$x^{T} A x=\sum_{i=1}^{n} x_{i}(A x)_{i}=\sum_{i=1}^{n} x_{i}\left(\sum_{j=1}^{n} A_{i j} x_{j}\right)=\sum_{i=1}^{n} \sum_{j=1}^{n} A_{i j} x_{i} x_{j}$$

$$x^{T} A x=\left(x^{T} A x\right)^{T}=x^{T} A^{T} x=x^{T}\left(\frac{1}{2} A+\frac{1}{2} A^{T}\right) x$$

我们经常隐含地假设以二次型出现的矩阵是对称阵。

• 对于所有非零向量$x \in \mathbb{R}^n$，$x^TAx>0$，对称阵$A \in \mathbb{S}^n$为正定（positive definite,PD）。这通常表示为$A\succ0$（或$A>0$），并且通常将所有正定矩阵的集合表示为$\mathbb{S}_{++}^n$。

• 对于所有向量$x^TAx\geq 0$，对称矩阵$A \in \mathbb{S}^n$是半正定(positive semidefinite ,PSD)。 这写为（或$A \succeq 0$仅$A≥0$），并且所有半正定矩阵的集合通常表示为$\mathbb{S}_+^n$。

• 同样，对称矩阵$A \in \mathbb{S}^n$是负定（negative definite,ND），如果对于所有非零$x \in \mathbb{R}^n$，则$x^TAx <0$表示为$A\prec0$（或$A <0$）。

• 类似地，对称矩阵$A \in \mathbb{S}^n$是半负定(negative semidefinite,NSD），如果对于所有$x \in \mathbb{R}^n$，则$x^TAx \leq 0$表示为$A\preceq 0$（或$A≤0$）。

• 最后，对称矩阵$A \in \mathbb{S}^n$是不定的，如果它既不是正半定也不是负半定，即，如果存在$x_1,x_2 \in \mathbb{R}^n$，那么$x_1^TAx_1>0$且$x_2^TAx_2<0$。

给定矩阵$A \in \mathbb{R}^{m \times n}$，矩阵$G = A^T A$（有时称为Gram矩阵）总是半正定的。 此外，如果$m\geq n$（同时为了方便起见，我们假设$A$是满秩），则$G = A^T A$是正定的。

3.12 特征值和特征向量

给定一个方阵$A \in\mathbb{R}^{n\times n}$，我们认为在以下条件下，$\lambda \in\mathbb{C}$是$A$的特征值，$x\in\mathbb{C}^n$是相应的特征向量：

$$Ax=\lambda x,x \ne 0$$

• 设$\lambda$是$A$的一个特征值，则 ${kA},{aA} + {bE},A^{2},A^{m},f(A),A^{T},A^{- 1}$有一个特征值分别为
  ${kλ},{aλ} + b,\lambda^{2},\lambda^{m},f(\lambda),\lambda,\lambda^{- 1},$ 且对应特征向量相同（$A^{T}$ 例外）

• 若$\lambda_{1},\lambda_{2},\cdots,\lambda_{n}$为$A$的$n$个特征值，则$\sum_{i= 1}^{n}\lambda_{i} = \sum_{i = 1}^{n}a_,\prod_{i = 1}^{n}\lambda_{i}= |A|$ ,从而$|A| \neq 0 \Leftrightarrow A$没有特征值

Jordan block

Let $A \in M_{n \times n}(C)$ and $v \in C^{n}$ be a generalized eigenvector of $A$ corresponding to the eigenvalue $\lambda$.

Suppose that $p$ is the smallest positive integer such that $\left(A-\lambda I_{n}\right)^{p}(\boldsymbol{v})=\boldsymbol{0}$. Let $\gamma=\left\{\left(A-\lambda I_{n}\right)^{p-1}(\boldsymbol{v}), \cdots,\left(A-\lambda I_{n}\right)(\boldsymbol{v}), \boldsymbol{v}\right\}$. Then

$$[A]_{\gamma}=\left(\begin{array}{ccccc}\lambda & 1 & 0 & \cdots & 0 \\ 0 & \lambda & 1 & \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & 0 \\ \vdots & & \ddots & \lambda & 1 \\ 0 & \cdots & 0 & 0 & \lambda\end{array}\right)$$

【Example】

Consider $A=\left(\begin{array}{ccc}3 & 1 & 0 \ -1 & 1 & 0 \ 3 & 2 & 2\end{array}\right)$. Its characteristic polynomial is $\operatorname{det}\left(\lambda I_{3}-A\right)=(\lambda-2)^{3}$.

There is 1 eigenvalue $\lambda=2$ (multiplicity $=3$ ).

Consider

$$E_{2}=N\left(A-2 I_{3}\right)=N\left(\begin{array}{ccc}1 & 1 & 0 \\ -1 & -1 & 0 \\ 3 & 2 & 0\end{array}\right)=\operatorname{span}\left\{\left(\begin{array}{l}0 \\ 0 \\ 1\end{array}\right)\right\}$$

Since $\operatorname{dim} E_{2}=1 \neq 3$ (multiplicity of $\left.\lambda=2\right), A$ is not diagonalizable.

Extend $E_{2}$ to

$$K_{2}=N\left(\left(A-2 I_{5}\right)^{2}\right)=N\left(\begin{array}{lll}0 & 0 & 0 \\ 0 & 0 & 0 \\ 1 & 1 & 0\end{array}\right)=\operatorname{span}\left\{\left(\begin{array}{l}0 \\ 0 \\ 1\end{array}\right),\left(\begin{array}{c}1 \\ -1 \\ 0\end{array}\right)\right\}, \operatorname{dim} K_{2}=2 \neq 3$$

The generalized eigenspace $K_2$ is not large enough to provide 3 eigenvectors. Let us consider

$$N\left(\left(A-2 I_{3}\right)^{3}\right)=N\left(\begin{array}{lll}0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0\end{array}\right)=C^3$$

which has dimension 3. Choose a vector, say

$$\left(\begin{array}{l}1 \\ 0 \\ 0\end{array}\right) \in N\left(\left(A-2 I_{3}\right)^{3}\right) \backslash N\left(\left(A-2 I_{3}\right)^{2}\right)$$

$AP=PJ\Rightarrow(AP_1,AP_2AP_3)=(2P_1,P_1+2P_2,P_2+2P_3)$

$$\left\{\begin{array}{lcl}AP_1&=&2P_1\\AP_2&=&P_1+2P_2\\AP_3&=&P_2+2P_3\end{array}\right.\Rightarrow \left\{\begin{array}{lcl}(A-2I_3)P_1&=&0\\(A-2I_3)P_2&=&P_1\\(A-2I_3)P_3&=&P_2\end{array}\right.$$

Then $P=\left\{(A-2I_3)^2\left(\begin{array}{l}1 \ 0 \ 0\end{array}\right)=\left(\begin{array}{l}0 \ 0 \ 1\end{array}\right),(A-2I_3)\left(\begin{array}{l}1 \ 0 \ 0\end{array}\right)=\left(\begin{array}{l}1 \ -1 \ 3\end{array}\right),\left(\begin{array}{l}1 \ 0 \ 0\end{array}\right) \right\}$ will form a basis of $C^3$. We have

$$\begin{aligned} \left(\begin{array}{ccc} 3 & 1 & 0 \\ -1 & 1 & 0 \\ 3 & 2 & 2 \end{array}\right) &=\left(\begin{array}{ccc} 0 & 1 & 1 \\ 0 & -1 & 0 \\ 1 & 3 & 0 \end{array}\right)\left(\begin{array}{lll} 2 & 1 & 0 \\ 0 & 2 & 1 \\ 0 & 0 & 2 \end{array}\right)\left(\begin{array}{ccc} 0 & 1 & 1 \\ 0 & -1 & 0 \\ 1 & 3 & 0 \end{array}\right)^{-1} \\ &=\left(\begin{array}{ccc} 0 & 1 & 1 \\ 0 & -1 & 0 \\ 1 & 3 & 0 \end{array}\right)\left(\begin{array}{ccc} 2 & 1 & 0 \\ 0 & 2 & 1 \\ 0 & 0 & 2 \end{array}\right)\left(\begin{array}{ccc} 0 & 3 & 1 \\ 0 & -1 & 0 \\ 1 & 1 & 0 \end{array}\right) \end{aligned}$$

【特殊的例题】

Let $M_{2 n \times 2 n}=\left(\begin{array}{ll}A_{n \times n} & B_{n \times n} \ C_{n \times n} & D_{n \times n}\end{array}\right)$ be a $2 n \times 2 n$ matrix such that $A_{n \times n}+B_{n \times n}=C_{n \times n}+D_{n \times n}$. Then the characteristic polynomial of $M_{2 n \times 2 n}$ is

$$\operatorname{det}\left(\lambda I_{2 n}-M_{2 n \times 2 n}\right)=\operatorname{det}\left(\lambda I_{n}-\left(A_{n \times n}-C_{n \times n}\right)\right) \operatorname{det}\left(\lambda I_{n}-\left(C_{n \times n}+D_{n \times n}\right)\right)$$

4.矩阵微积分

4.1 梯度

假设$f: \mathbb{R}^{m \times n} \rightarrow \mathbb{R}$是将维度为$m \times n$的矩阵$A\in \mathbb{R}^{m \times n}$作为输入并返回实数值的函数。 然后$f$的梯度是偏导数矩阵，定义如下：

$$\nabla_{A} f(A) \in \mathbb{R}^{m \times n}=\left[\begin{array}{cccc}{\frac{\partial f(A)}{\partial A_{11}}} & {\frac{\partial f(A)}{\partial A_{12}}} & {\cdots} & {\frac{\partial f(A)}{\partial A_{1n}}} \\ {\frac{\partial f(A)}{\partial A_{21}}} & {\frac{\partial f(A)}{\partial A_{22}}} & {\cdots} & {\frac{\partial f(A)}{\partial A_{2 n}}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {\frac{\partial f(A)}{\partial A_{m 1}}} & {\frac{\partial f(A)}{\partial A_{m 2}}} & {\cdots} & {\frac{\partial f(A)}{\partial A_{m n}}}\end{array}\right]$$

如果$A$只是向量$A\in \mathbb{R}^{n}$，则

$$\nabla_{x} f(x)=\left[\begin{array}{c}{\frac{\partial f(x)}{\partial x_{1}}} \\ {\frac{\partial f(x)}{\partial x_{2}}} \\ {\vdots} \\ {\frac{\partial f(x)}{\partial x_{n}}}\end{array}\right]$$

从偏导数的等价性质得出：

• $\nabla_{x}(f(x)+g(x))=\nabla_{x} f(x)+\nabla_{x} g(x)$

• 对于$t \in \mathbb{R}$ ，$\nabla_{x}(t f(x))=t \nabla_{x} f(x)$

4.2 黑塞矩阵

假设$f: \mathbb{R}^{n} \rightarrow \mathbb{R}$是一个函数，它接受$\mathbb{R}^{n}$中的向量并返回实数。那么关于$x$的黑塞矩阵（也有翻译作海森矩阵），写做：$\nabla_x ^2 f(A x)$，或者简单地说，$H$是$n \times n$矩阵的偏导数：

$$\nabla_{x}^{2} f(x) \in \mathbb{R}^{n \times n}=\left[\begin{array}{cccc}{\frac{\partial^{2} f(x)}{\partial x_{1}^{2}}} & {\frac{\partial^{2} f(x)}{\partial x_{1} \partial x_{2}}} & {\cdots} & {\frac{\partial^{2} f(x)}{\partial x_{1} \partial x_{n}}} \\ {\frac{\partial^{2} f(x)}{\partial x_{2} \partial x_{1}}} & {\frac{\partial^{2} f(x)}{\partial x_{2}^{2}}} & {\cdots} & {\frac{\partial^{2} f(x)}{\partial x_{2} \partial x_{n}}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {\frac{\partial^{2} f(x)}{\partial x_{n} \partial x_{1}}} & {\frac{\partial^{2} f(x)}{\partial x_{n} \partial x_{2}}} & {\cdots} & {\frac{\partial^{2} f(x)}{\partial x_{n}^{2}}}\end{array}\right]$$

4.3 朗斯基行列式 Wronskian

$$W\left(f_{1}, \cdots, f_{n}\right)(x)=\left|\begin{array}{cccc} f_{1}(x) & f_{2}(x) & \cdots & f_{n}(x) \\ f_{1}^{\prime}(x) & f_{2}^{\prime}(x) & \cdots & f_{n}^{\prime}(x) \\ \vdots & \vdots & \ddots & \vdots \\ f_{1}^{(n-1)}(x) & f_{2}^{(n-1)}(x) & \cdots & f_{n}^{(n-1)}(x) \end{array}\right|$$

$W\left(f_{1}, \cdots, f_{n}\right)(x) \neq 0$ if and only if $f_{1}, \cdots, f_{n}$ are linearly independent.

5. Linear Transformations

5.1 Transformations

做矩阵乘法可以看作是对一个矩阵做基的转换。给定一个方阵$A \in\mathbb{R}^{2\times 2}$，以 $AI_2$ 为例

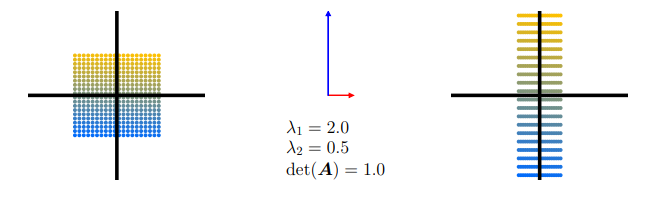
1. $\boldsymbol{A}_{1}=\left[\begin{array}{ll}\frac{1}{2} & 0 \ 0 & 2\end{array}\right]$ 两个特征向量的方向与 $\mathbb{R}^{2}$ 中的标准基向量相同，即在两个主轴上。纵轴延长2倍（特征值$ \lambda_{1}=2$）。 横轴压缩 $\frac{1}{2}$ 倍（特征值 $ \lambda_{2}=\frac{1}{2}$）。该映射不会改变原图形面积$\operatorname{det}\left(\boldsymbol{A}_{1}\right)=1=2 \cdot \frac{1}{2}$

   

2. $\boldsymbol{A}_{2}=\left[\begin{array}{ll}1 & \frac{1}{2} \ 0 & 1\end{array}\right]$ 对应于剪切映射( shearing mapping)，即如果点位于垂直轴的正半轴，则沿水平轴向右剪切点，反之亦然。这个映射不改变原图形的面积 ( $\operatorname{det}\left(\boldsymbol{A}_{2}\right)=1$)。特征值重复 $\lambda_{1}=1=\lambda_{2}$ ，且特征向量共线 (此处的绘制强调的是两个相反方向)。这表示映射仅沿一个方向 (水平轴) 起作用。

   

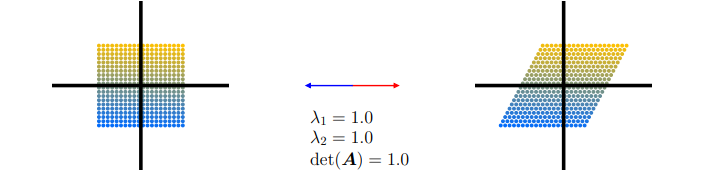
3. $\boldsymbol{A}_{3}=\left[\begin{array}{cc}\cos \left(\frac{\pi}{6}\right) & -\sin \left(\frac{\pi}{6}\right) \ \sin \left(\frac{\pi}{6}\right) & \cos \left(\frac{\pi}{6}\right)\end{array}\right]=\frac{1}{2}\left[\begin{array}{cc}\sqrt{3} & -1 \ 1 & \sqrt{3}\end{array}\right]$ 矩阵 $\boldsymbol{A}_{3} $ 将原图形的点逆时针旋转 $ \frac{\pi}{6} \mathrm{rad}=30^{\circ}$ ，并且只有复数的特征值，这反映出映射是旋转 (因此，没有绘制特征向量)。旋转必须保持体积不变，所以行列式是1。

   

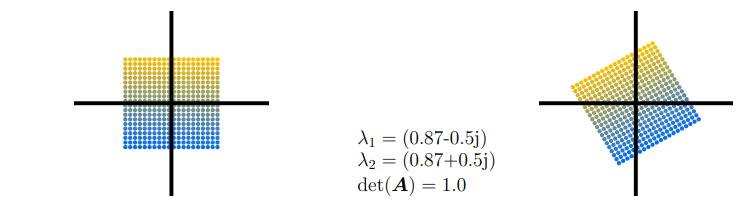
4. $\boldsymbol{A}_{4}=\left[\begin{array}{cc}1 & -1 \ -1 & 1\end{array}\right]$ 表示将二维域折叠到一维的标准基映射。由于有一个特征值为 0 ，与 $\lambda_{1}=0$ 对应的 (蓝色) 特征向量方向上的空间收缩为 0 ，而与蓝色正交的 (红色) 特征向量将空间拉伸 $\lambda_{2}=2$ 倍。因此，图像的面积为 0 。

   

5. $\boldsymbol{A}_{5}=\left[\begin{array}{cc}1 & \frac{1}{2} \ \frac{1}{2} & 1\end{array}\right]$ 是一种剪切和拉伸映射，它将空间缩放 75% ，因为 $\left|\operatorname{det}\left(\mathrm{A}_{5}\right)\right|=\frac{3}{4}$。它将空间沿 $\lambda_{2}$ 的 (红色) 特征向量方向拉伸1.5倍，并沿与红色正交的 (蓝色) 特征向量方向压缩0.5倍。

   

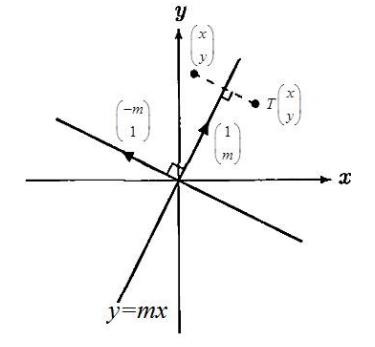
5.3 Projection

Let $T: \boldsymbol{R}^{2} \rightarrow \boldsymbol{R}^{2}$ be linear transformation defined by $T\left(\begin{array}{c}1 \ m\end{array}\right)=\left(\begin{array}{c}1 \ m\end{array}\right)$ and $ T\left(\begin{array}{c}-m \ 1\end{array}\right)=\left(\begin{array}{l}0 \ 0\end{array}\right) $

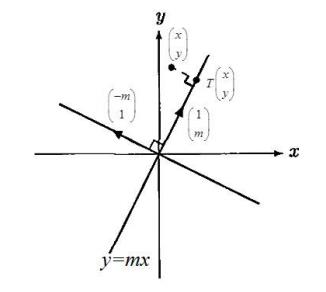
Method 1 :

Since $\text{det}\left(\begin{array}{cc}1 & -m \ m & 1\end{array}\right)=1+m^{2} \neq 0$,$\left\{\left(\begin{array}{c}1 \\m\end{array}\right),\left(\begin{array}{c}-m \ 1\end{array}\right)\right\}$ is linearly independent. Hence $\left\{\left(\begin{array}{c}1 \ m\end{array}\right),\left(\begin{array}{c}-m \ 1\end{array}\right)\right\}$ is a basis of $\boldsymbol{R}^{2}$ . Consider

$$\left(\begin{array}{l}1 \\0\end{array}\right)=a\left(\begin{array}{c}1 \\m\end{array}\right)+b\left(\begin{array}{c}-m \\1\end{array}\right) \text { and }\left(\begin{array}{l}0 \\1\end{array}\right)=c\left(\begin{array}{c}1 \\m\end{array}\right)+d\left(\begin{array}{c}-m \\1\end{array}\right)$$

That is

$$\left(\begin{array}{l}1 \\0\end{array}\right)=\left(\begin{array}{cc} 1 & -m \\m & 1\end{array}\right)\left(\begin{array}{l} a \\b\end{array}\right) \text { and }\left(\begin{array}{l}0\\1\end{array}\right)=\left(\begin{array}{cc}1 & -m \\m & 1\end{array}\right)\left(\begin{array}{l}c \\d\end{array}\right)$$

By Cramer’s rule,

$$\begin{aligned} a=\frac{\left|\begin{array}{cc}1 & -m \\0 & 1\end{array}\right|}{\left|\begin{array}{cc}1 & -m \\m & 1\end{array}\right|}=\frac{1}{1+m^{2}} \quad b=\frac{\left|\begin{array}{cc}1 & 1 \\m & 0\end{array}\right|}{\left|\begin{array}{cc}1 & -m \\m & 1 \end{array}\right|}=\frac{-m}{1+m^{2}}\\ \\ c=\frac{\left|\begin{array}{cc}0 & -m \\1 & 1\end{array}\right|}{\left|\begin{array}{cc}1 & -m \\m & 1\end{array}\right|}=\frac{m}{1+m^{2}} \quad d=\frac{\left|\begin{array}{cc}1 & 0 \\m & 1\end{array}\right|}{\left|\begin{array}{cc}1 & -m \\m & 1\end{array}\right|}=\frac{1}{1+m^{2}} \end{aligned}$$

Then

$$\begin{aligned} \left(\begin{array}{l}1 \\0\end{array}\right) = \frac{1}{1+m^{2}}\left(\begin{array}{c}1 \\m\end{array}\right)-\frac{m}{1+m^{2}}\left(\begin{array}{c}-m \\1\end{array}\right)\\ \left(\begin{array}{l}0 \\1\end{array}\right) = \frac{m}{1+m^{2}}\left(\begin{array}{c}1 \\m\end{array}\right)+\frac{1}{1+m^{2}}\left(\begin{array}{c}-m \\1\end{array}\right) \end{aligned}$$ $$\begin{aligned} T\left(\begin{array}{l}1 \\0\end{array}\right) & = T\left(\frac{1}{1+m^{2}}\left(\begin{array}{c}1 \\m\end{array}\right)-\frac{m}{1+m^{2}}\left(\begin{array}{c}-m\\1\end{array}\right)\right)\\ & = \frac{1}{1+m^{2}} T\left(\begin{array}{c}1 \\m\end{array}\right)-\frac{m}{1+m^{2}} T\left(\begin{array}{c}-m \\1\end{array}\right)\\ & = \frac{1}{1+m^{2}}\left(\begin{array}{c}1 \\m\end{array}\right)\\ & = \left(\begin{array}{c}\frac{1}{1+m^{2}} \\ \frac{m}{1+m^{2}}\end{array}\right)\\ & = \frac{1}{1+m^{2}}\left(\begin{array}{l}1 \\0\end{array}\right)+\frac{m}{1+m^{2}}\left(\begin{array}{l}0 \\1\end{array}\right) \end{aligned}$$ $$\begin{aligned} T\left(\begin{array}{l}0\\1\end{array}\right) & = T\left(\frac{m}{1+m^{2}}\left(\begin{array}{c}1 \\m\end{array}\right)+\frac{1}{1+m^{2}}\left(\begin{array}{c}-m \\1\end{array}\right)\right)\\ & = \frac{m}{1+m^{2}} T\left(\begin{array}{c}1 \\m\end{array}\right)+\frac{1}{1+m^{2}} T\left(\begin{array}{c}-m \\1\end{array}\right)\\ & = \frac{m}{1+m^{2}}\left(\begin{array}{c}1 \\m\end{array}\right)\\ & = \left(\begin{array}{c}\frac{m}{1+m^{2}} \\ \frac{m^{2}}{1+m^{2}}\end{array}\right)\\ & = \frac{m}{1+m^{2}}\left(\begin{array}{l}1 \\0\end{array}\right)+\frac{m^{2}}{1+m^{2}}\left(\begin{array}{l}0 \\1\end{array}\right) \end{aligned}$$ $$\begin{aligned} {\left[T^{2}\right]_{\beta} } &=\left([T]_{\beta}\right)^{2} \\ &=\left(\begin{array}{ll} \frac{1}{1+m^{2}} & \frac{m}{1+m^{2}} \\ \frac{m}{1+m^{2}} & \frac{m^{2}}{1+m^{2}} \end{array}\right)\left(\begin{array}{cc} \frac{1}{1+m^{2}} & \frac{m}{1+m^{2}} \\ \frac{m}{1+m^{2}} & \frac{m^{2}}{1+m^{2}} \end{array}\right) \\ &=\left(\begin{array}{ll} \frac{1+m^{2}}{\left(1+m^{2}\right)^{2}} & \frac{m+m^{3}}{\left(1+m^{2}\right)^{2}} \\ \frac{m+m^{3}}{\left(1+m^{2}\right)^{2}} & \frac{m^{2}+m^{4}}{\left(1+m^{2}\right)^{2}} \end{array}\right) \\ &=\left(\begin{array}{ll} \frac{1}{1+m^{2}} & \frac{m}{1+m^{2}} \\ \frac{m}{1+m^{2}} & \frac{m^{2}}{1+m^{2}} \end{array}\right)=[T]_{\beta} \end{aligned}$$

Method 2 :

$$\boldsymbol{p}=\frac{(x, y)\left(\begin{array}{c}1 \\m\end{array}\right)}{(1, m)\left(\begin{array}{c}1 \\m\end{array}\right)}\left(\begin{array}{c}1 \\m\end{array}\right)=\frac{x+m y}{1+m^{2}}\left(\begin{array}{c}1 \\m\end{array}\right)=\left(\begin{array}{cc}\frac{1}{1+m^{2}} & \frac{m}{1+m^{2}} \\ \frac{m}{1+m^{2}} & \frac{m^{2}}{1+m^{2}}\end{array}\right)\left(\begin{array}{l}x \\y\end{array}\right)$$ $$\begin{aligned} \boldsymbol{x}-\boldsymbol{p}&=\left(\begin{array}{l}x \\y\end{array}\right)-\frac{x+m y}{1+m^{2}}\left(\begin{array}{c}1 \\m\end{array}\right)\\ &=\left(\begin{array}{c} x-\frac{x+m y}{1+m^{2}} \\ y-m \frac{x+m y}{1+m^{2}} \end{array}\right)\\ &=\left(\begin{array}{c} \frac{x\left(1+m^{2}\right)-(x+m y)}{1+m^{2}} \\ \frac{y\left(1+m^{2}\right)-\left(m x+m^{2} y\right)}{1+m^{2}} \end{array}\right)\\ &=\left(\begin{array}{c} \frac{x m^{2}-m y}{1+m^{2}} \\ \frac{y-m x}{1+m^{2}} \end{array}\right)\\ &=\frac{y-m x}{1+m^{2}}\left(\begin{array}{c}-m \\1\end{array}\right)\\ &=\frac{(x, y)\left(\begin{array}{c}-m \\1\end{array}\right)}{(-m, 1)\left(\begin{array}{c}-m \\1\end{array}\right)}\left(\begin{array}{c}-m \\1\end{array}\right) \in W^{\perp} \end{aligned}$$

So, $\boldsymbol{x}-\boldsymbol{p}=\text{proj}_{W^{\perp}}\left(\begin{array}{l}x \\y\end{array}\right)$ and $\boldsymbol{x}=\text{proj}_{W}\left(\begin{array}{l}x \\y\end{array}\right)+\text{proj}_{W^{\perp}}\left(\begin{array}{l}x \\y\end{array}\right)$

5.3 Reflection

Let $T: \boldsymbol{R}^{2} \rightarrow \boldsymbol{R}^{2}$ be linear transformation defined by $T\left(\begin{array}{c}1 \ m\end{array}\right)=\left(\begin{array}{c}1 \ m\end{array}\right)$ and $ T\left(\begin{array}{c}-m \ 1\end{array}\right)=\left(\begin{array}{l}m \ -1\end{array}\right) $

$$\begin{aligned} T\left(\begin{array}{l}1 \\0\end{array}\right) & = T\left(\frac{1}{1+m^{2}}\left(\begin{array}{c}1 \\m\end{array}\right)-\frac{m}{1+m^{2}}\left(\begin{array}{c}-m\\1\end{array}\right)\right)\\ & = \frac{1}{1+m^{2}} T\left(\begin{array}{c}1 \\m\end{array}\right)-\frac{m}{1+m^{2}} T\left(\begin{array}{c}-m \\1\end{array}\right)\\ & = \frac{1}{1+m^{2}}\left(\begin{array}{c}1 \\m\end{array}\right)-\frac{m}{1+m^{2}}\left(\begin{array}{c}m \\-1\end{array}\right)\\ & = \left(\begin{array}{c}\frac{1-m^{2}}{1+m^{2}} \\ \frac{2 m}{1+m^{2}}\end{array}\right)\\ & = \frac{1-m^{2}}{1+m^{2}}\left(\begin{array}{l}1 \\0\end{array}\right)+\frac{2 m}{1+m^{2}}\left(\begin{array}{l}0 \\1\end{array}\right) \end{aligned}$$ $$\begin{aligned} T\left(\begin{array}{l}0\\1\end{array}\right) & = T\left(\frac{m}{1+m^{2}}\left(\begin{array}{c}1 \\m\end{array}\right)+\frac{1}{1+m^{2}}\left(\begin{array}{c}-m \\1\end{array}\right)\right)\\ & = \frac{m}{1+m^{2}} T\left(\begin{array}{c}1 \\m\end{array}\right)+\frac{1}{1+m^{2}} T\left(\begin{array}{c}-m \\1\end{array}\right)\\ & = \frac{m}{1+m^{2}}\left(\begin{array}{c}1 \\m\end{array}\right)+\frac{1}{1+m^{2}}\left(\begin{array}{c}m \\-1\end{array}\right)\\ & = \left(\begin{array}{c}\frac{2 m}{1+m^{2}} \\-\frac{1-m^{2}}{1+m^{2}}\end{array}\right)\\ & = \frac{2 m}{1+m^{2}}\left(\begin{array}{l}1 \\0\end{array}\right)-\frac{1-m^{2}}{1+m^{2}}\left(\begin{array}{l}0 \\1\end{array}\right) \end{aligned}$$ $$\begin{aligned} {\left[T^{2}\right]_{\beta} } &=\left([T]_{\beta}\right)^{2} \\ &=\left(\begin{array}{cc} \frac{1-m^{2}}{1+m^{2}} & \frac{2 m}{1+m^{2}} \\ \frac{2 m}{1+m^{2}} & -\frac{1-m^{2}}{1+m^{2}} \end{array}\right)\left(\begin{array}{cc} \frac{1-m^{2}}{1+m^{2}} & \frac{2 m}{1+m^{2}} \\ \frac{2 m}{1+m^{2}} & -\frac{1-m^{2}}{1+m^{2}} \end{array}\right) \\ &=\left(\begin{array}{cc} \frac{\left(1-m^{2}\right)^{2}+(2 m)^{2}}{\left(1+m^{2}\right)^{2}} & \frac{2 m\left(1-m^{2}\right)-\left(1-m^{2}\right) 2 m}{\left(1+m^{2}\right)^{2}} \\ \frac{2 m\left(1-m^{2}\right)-\left(1-m^{2}\right) 2 m}{\left(1+m^{2}\right)^{2}} & \frac{\left(1-m^{2}\right)^{2}+(2 m)^{2}}{\left(1+m^{2}\right)^{2}} \end{array}\right) \\ &=\left(\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right) \end{aligned}$$