【笔记】高等数学复习笔记-微积分

基于 ChiuFai WONG 教授的线性代数课件的笔记；

与网上资料结合进行整理；

对于部分基础多有忽略，主要用于知识点查找；

函数的可导性与连续性之间的关系

Th1: 函数$f(x)$在$x_0$处可微$\Leftrightarrow f(x)$在$x_0$处可导

Th2: 若函数在点$x_0$处可导，则$y=f(x)$在点$x_0$处连续，反之则不成立。即函数连续不一定可导。

Th3: $f’(x_{0})$存在$\Leftrightarrow f’_{-}(x_{0})=f’_{+}(x_{0})$

平面曲线的切线和法线

切线方程 : $y-y_{0}=f’(x_{0})(x-x_{0})$

法线方程：$y-y_{0}=-\frac{1}{f’(x_{0})}(x-x_{0}),f’(x_{0})\ne 0$

渐近线的求法

1. 水平渐近线 若$\underset{x\to +\infty }{\mathop{\lim }}\,f(x)=b$，或$\underset{x\to -\infty }{\mathop{\lim }}\,f(x)=b$，则

   $y=b$称为函数$y=f(x)$的水平渐近线。

2. 铅直渐近线 若$\underset{x\to x_{0}^{-}}{\mathop{\lim }}\,f(x)=\infty $，或$\underset{x\to x_{0}^{+}}{\mathop{\lim }}\,f(x)=\infty $，则

   $x=x_{0}$称为$y=f(x)$的铅直渐近线。

3. 斜渐近线 若$a=\underset{x\to \infty }{\mathop{\lim }}\,\frac{f(x)}{x},\quad b=\underset{x\to \infty }{\mathop{\lim }}\,[f(x)-ax]$，则$

   y=ax+b$称为$y=f(x)$的斜渐近线。

函数凹凸性的判断

Th1: (凹凸性的判别定理）若在 I 上$f’’(x)<0$（或$f''(x)>0$），则$f(x)$在 I 上是凸的（或凹的）。

Th2: (拐点的判别定理 1）若在$x_{0}$处$f’’(x)=0$，（或$f’’(x)$不存在），当$x$变动经过$x_{0}$时，$f’’(x)$变号，则$(x_{0},f(x_{0}))$为拐点。

Th3: (拐点的判别定理 2）设$f(x)$在$x_{0}$点的某邻域内有三阶导数，且$f’’(x)=0$，$f’’’(x)\ne 0$，则$(x_{0},f(x_{0}))$为拐点。

四则运算法则

设函数$u=u(x)，v=v(x)$在点$x$可导则

1. $(u\pm v{)}’={u}’\pm {v}’$ $d(u\pm v)=du\pm dv$
2. $(uv{)}’=u{v}’+v{u}’$ $d(uv)=udv+vdu$
3. $(\frac{u}{v}{)}’=\frac{v{u}’-u{v}’}{v^{2}}(v\ne 0)$ $d(\frac{u}{v})=\frac{vdu-udv}{v^{2}}$

微分中值定理

费马定理

函数$f(x)$在$x_{0}$的某邻域内有定义，并且在此邻域内恒有 $f(x)\le f(x_{0})$或 $f(x)\ge f(x_{0})$，且 $f(x)$在$x_{0}$处可导,则有 ${f}’(x_{0})=0$

罗尔定理 Rolle’s Theorem

Let $f$ be continuous on a closed interval $[a, b]$ and differentiable on $(a, b)$ with $f (a) = f (b)$ . There is at least one point $c$ in $(a, b)$ such that $f’(x)=0$

拉格朗日中值定理 Lagrange Mean Value Theorem

Let $f$ be continuous on a closed interval $[a, b]$ and differentiable on $(a, b)$ , then there is at least one point $x$ in $(a, b)$ such that

$$\frac{f(b)-f(a)}{b-a}=f'(x)$$

柯西中值定理 Cauchy mean value theorem

Let $f，g$ be continuous on a closed interval $[a, b]$ and differentiable on $(a, b)$ with ${g}’(x)\ne 0$，then there is at least one point $x$ in $(a, b)$ such that

$$\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f'(x)}{g'(x)}$$

洛必达法则 L’Hôpital’s Rule

$0/0$ 型

Suppose $f$ and $g$ are differentiable on an open interval $I$ containing $a$ with $g(x)\ne 0$ on $I$ . when $x\ne a$ .

If $\lim_{x\to a}f(x)=\lim_{x\to a}g(x)=0$, then

$$\lim_{x\to a}\frac{f(x)}{g(x)}=\lim_{x\to a}\frac{f'(x)}{g'(x)}$$

Proof:

$$f(x)\approx f'(a)(x-a)\qquad g(x)\approx g'(a)(x-a)$$ $$\frac{f(x)}{g(x)}\approx\frac{f'(x)(x-a)}{g'(x)(x-a)}=\frac{f'(x)}{g'(x)}$$

$\infty/\infty$ 型

If $\lim_{x\to a}f(x)=\pm\infty$ and $\lim_{x\to a}g(x)=\pm\infty$, then

$$\lim_{x\to a}\frac{f(x)}{g(x)}=\lim_{x\to a}\frac{f'(x)}{g'(x)}$$

Proof:

Let $F(x)=f(x)^{-1}$ and $G(x)=g(x)^{-1}$. Then $\lim_{x\to a}F(x)=\lim_{x\to a}G(x)=0$

$$\lim_{x\to a}\frac{f(x)}{g(x)}=\lim_{x\to a}\frac{G(x)}{F(x)}=\lim_{x\to a}\frac{G'(x)}{F'(x)}=\lim_{x\to a}\frac{-g'(x)^{-2}g'(x)}{-f'(x)^{-2}f'(x)}=\lim_{x\to a}\frac{f'(x)^{2}g'(x)}{g'(x)^{2}f'(x)}=\lim_{x\to a}\frac{f'(x)}{g'(x)}$$

特殊情况中转换成 $0/0$ 型的方法

1. $0\cdot\infty: \lim_{x\to a}\underbrace{f(x)}_{\to0}\underbrace{g(x)}_{\to\infty}=\lim_{x\to a}\frac{\overbrace{f(x)}^{\to0}}{\underbrace{g(x)^{-1}}_{\to0}}$
2. $\infty-\infty: \lim_{x\to a}(\underbrace{f(x)}_{\to\infty}-\underbrace{g(x)}_{\to\infty})=\lim_{x\to a}(\underbrace{\frac1{f(x)^{-1}}}_{\to0}-\underbrace{\frac1{g(x)^{-1}}}_{\to0})=\lim_{x\to a}\frac{\overbrace{g(x)^{-1}-f(x)^{-1}}^{\to0}}{\underbrace{f(x)^{-1}g(x)^{-1}}_{\to0}}$
3. $0^{0}: \lim _{x \to a} \underbrace{f(x)^{\overbrace{g(x)}^{\to 0}}}_{\to 0}=\lim _{x \to a} e^{\overbrace{g(x)}^{\to0} \overbrace{\ln f(x)}^{\to -\infty}}=e^{\lim_{x\to a}\overbrace{g(x)}^{\to0} \overbrace{\ln f(x)}^{\to -\infty}}$ reduced to case (1);
4. $1^{\infty}: \lim _{x \to a} \underbrace{f(x)^{\overbrace{g(x)}^{\to \infty}}}_{\to 1}=\lim _{x \to a} e^{\overbrace{g(x)}^{\to\infty} \overbrace{\ln f(x)}^{\to0}}=e^{\lim_{x\to a}\overbrace{g(x)}^{\to\infty} \overbrace{\ln f(x)}^{\to 0}}$ reduced to case (1);
5. $\infty ^{0}: \lim _{x \to a} \underbrace{f(x)^{\overbrace{g(x)}^{\to 0}}}_{\to 0}=\lim _{x \to a} e^{\overbrace{g(x)}^{\to0} \overbrace{\ln f(x)}^{\to \infty}}=e^{\lim_{x\to a}\overbrace{g(x)}^{\to0} \overbrace{\ln f(x)}^{\to \infty}}$ reduced to case (1);

泰勒公式

设函数$f(x)$在点$x_{0}$处的某邻域内具有$n+1$阶导数，则对该邻域内异于$x_{0}$的任意点$x$：

$$f(x)=f(x_{0})+f'(x_{0})(x-x_{0})+\frac{1}{2!}f''(x_{0})(x-x_{0})^{2}+\cdots+\frac{f^{(n)}(x_{0})}{n!}(x-x_{0})^{n}+R_{n}(x)$$

当 $x_0=0$ 时，为麦克劳林公式

Growth Rates of Functions (as $x\to\infty$)

Let $f\ll g$ mean that $g$ grows faster than $f$ as $x\to\infty$ . With positive real number $p, q, r, s$, and $a >1$,

$$(\ln x)^q\ll x^p\ll x^p(\ln x)^r\ll x^{p+s}\ll a^x\ll x^x$$

Growth Rates of Sequences

The following sequences are ordered according to increasing growth rates as $n\to\infty$; that is, if $\{a_n\}\ll\{b_n\}$ in the list, then $\lim_{n\to\infty}\frac{a_n}{b_n}=0$:

$$\{(\ln n)^q\}\ll\{n^p\}\ll\{n^p(\ln n)^r\}\ll\{n^{p+s}\}\ll\{a^n\}\ll\{n!\}\ll\{n^n\}$$

Integration by parts

the Product Rule states that

$$(uv)'=uv'+u'v$$

By integrating both sides, we have

$$uv=\int(uv)'dx=\int uv'dx+\int u'vdx=\int udv+\int vdu$$

Rearranging this expression, integration by parts for indefinite integral is

$$\int udv=uv-\int vdu$$

Similarly, integration by parts for definite integral is

$$\int_a^b uv'dx=uv\bigg |_a^b-\int_a^b vu'dx$$

Beta function

Let $m, n$ be two non-negative integers. Define

$$I_{m,n}=\int_0^1x^m(1-x)^ndx$$ $$I_{m,n}=\frac n{m+n+1}I_{m,n-1}\qquad I_{m,n}=\frac{m!n!}{(m+n+1)!}$$

Strategies for solving $\int\sin^mx \cos^nx dx$

(i) $\quad m=2 k+1$ odd, $n$ real

$$\begin{aligned} \int \sin ^{2 k+1} x \cos ^{n} x d x &=\int \sin ^{2 k} x \cos ^{n} x \sin x d x \\ &=\int\left(1-\cos ^{2} x\right)^{k} \cos ^{n} x \sin x d x \\ &=-\int\left(1-\cos ^{2} x\right)^{k} \cos ^{n} x d \cos x \end{aligned}$$

(ii) $m$ real, $n=2 l+1$ odd

$$\begin{aligned} \int \sin ^{m} x \cos ^{2 l+1} x d x &=\int \sin ^{m} x \cos ^{2 l} x \cos x d x \\ &=\int \sin ^{m} x\left(1-\sin ^{2} x\right)^{l} \cos x d x \\ &=\int \sin ^{m} x\left(1-\sin ^{2} x\right)^{l} d \sin x \end{aligned}$$

(iii) both $m=2 k$ and $n=2 l$ nonnegative even integers

Method 1:

Use $\sin ^{2} x=\frac{1-\cos 2 x}{2}$ and $\cos ^{2} x=\frac{1+\cos 2 x}{2}$ to transform $\sin ^{2 k} x \cos ^{2 l} x$ into a polynomial in $\cos 2 x$;

$$\int \sin ^{2 k} x \cos ^{2 l} x d x=\frac{1}{2^{k+l}} \int(1-\cos 2 x)^{k}(1+\cos 2 x)^{l} d x$$

and apply the preceding strategies once again to powers of $\cos 2 x$ greater than 1.

Method 2:

$$\quad \int \sin ^{2 k} x \cos ^{2 l} x d x=\int\left(1-\cos ^{2} x\right)^{k} \cos ^{2 l} x d x$$

and apply reduction formula (b) in Reduction Formulas for Power of Trigonometric Functions to each term on the right after expansion.

特殊例题

Exponential constant

$$\lim_{n\to\infty}(1+\frac1n)^n=e$$

Method 1:

$$\begin{aligned} \left(1+\frac{1}{n}\right)^{n}&=\left(\begin{array}{l} n \\ 0 \end{array}\right)+\left(\begin{array}{c} n \\ 1 \end{array}\right) \frac{1}{n}+\left(\begin{array}{c} n \\ 2 \end{array}\right) \frac{1}{n^{2}}+\cdots+\left(\begin{array}{l} n\\k\end{array}\right) \frac{1}{n^{k}}+\cdots+\left(\begin{array}{l} n\\n\end{array}\right) \frac{1}{n^{n}} \\ &=1+\frac{1}{1 !} \cdot \frac{n}{n}+\frac{1}{2 !} \cdot \frac{n(n-1)}{n^{2}}+\cdots+\frac{1}{k !} \cdot \frac{n(n-1) \cdots(n-k+1)}{n^{k}}+\cdots+\frac{1}{n !} \cdot \frac{n !}{n^{n}} \\ &=1+\frac{1}{1 !}+\frac{1}{2 !}\left(1-\frac{1}{n}\right)+\cdots+\frac{1}{k !}\left(1-\frac{1}{n}\right) \cdots\left(1-\frac{k-1}{n}\right)+\cdots+\frac{1}{n !} \cdot\left(1-\frac{1}{n}\right) \cdots\left(1-\frac{n-1}{n}\right) \\ \end{aligned}$$ $$\lim_{n\to\infty}(1+\frac1n)^n=1+\frac{1}{1 !}+\frac{1}{2 !} \cdots+\frac{1}{k !}+\cdots+\frac{1}{n !}=e$$

Method 2:

$$\ln (1+\frac1n)^n=n\cdot\ln(1+\frac1n)$$

By L’Hôpital’s rule

$$\lim_{n\to\infty}n\cdot\ln(1+\frac1n)=\lim_{n\to\infty}\frac{\ln(1+\frac1n)}{\frac1n}=\lim_{n\to\infty}\frac{-1}{(1+\frac1n)\cdot n^2}/\frac{-1}{n^2}=1$$ $$\lim_{n\to\infty}(1+\frac1n)^n=e$$

扩展:

$$1-\frac{1}{x}=\frac{x-1}{x}=\frac{1}{\left(\frac{x}{x-1}\right)}=\frac{1}{1+\frac{1}{x-1}}=(1+\frac{1}{x-1})^{-1}$$

Then

$$\lim _{x \rightarrow \infty}\left(1-\frac{1}{x}\right)^{-x}=\lim _{x \rightarrow \infty}\left(1+\frac{1}{x-1}\right)^{x}=\lim _{x \rightarrow \infty}\left(1+\frac{1}{x-1}\right)^{x-1} \cdot\left(1+\frac{1}{x-1}\right)=e$$

Furthermore

$$\lim _{y \rightarrow-\infty}\left(1+\frac{1}{y}\right)^{y}=\lim _{x \rightarrow \infty}\left(1-\frac{1}{x}\right)^{-x}=e$$

Squeeze Theorem 例题

$$\lim _{x \rightarrow 0} \frac{\sin x}{x}=1$$

Proof:

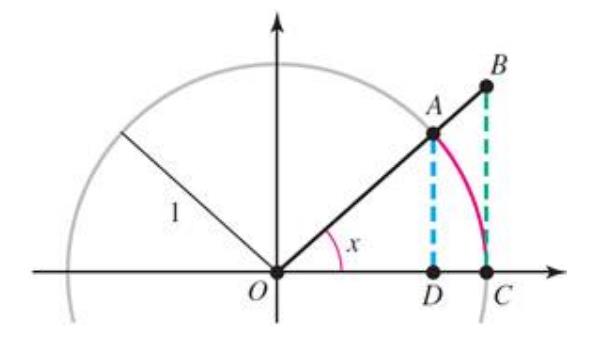
Area of $\Delta O A D=\frac{1}{2}(O D)(A D)=\frac{1}{2} \cos x \sin x $

$角度(x)=弧长/半径$ ，Area of sector $O A C=\frac{1}{2} \cdot 1^{2} \cdot x=\frac{x}{2} $

Area of $ \triangle O B C=\frac{1}{2}(O C)(B C)=\frac{1}{2} \tan x$

Since area of $\triangle O A D< $ area of $ O A C<$ area of $\triangle O B C$ , we have

$$\frac{1}{2} \cos x \sin x<\frac{x}{2}<\frac{1}{2} \tan x$$

Hence

$$\cos x<\frac{\sin x}{x}<\frac{1}{\cos x}$$

we find that

$$1=\lim _{x \rightarrow 0^{+}} \cos x<\lim _{x \rightarrow 0^{+}} \frac{\sin x}{x}<\lim _{x \rightarrow 0^{+}} \frac{1}{\cos x}=1$$

By Squeeze Theorem

$$\lim _{x \rightarrow 0^{+}} \frac{\sin x}{x}=1$$

Similarly

$$\lim _{x \rightarrow 0^{-}} \frac{\sin x}{x}=1$$

Therefore

$$\lim _{x \rightarrow 0} \frac{\sin x}{x}=1$$

$\ln$ 求导的辅助作用

$$d\ln f(x)=\frac{f'(x)}{f(x)}$$

可转换成以下方程求导

$$f'(x)=f(x)\times d\ln f(x)$$

公式查找表

常用泰勒公式

$$\begin{aligned}e^{x}&=1+x+\frac{1}{2 !} x^{2}+\cdots+\frac{1}{n !} x^{n}+o\left(x^{n}\right) \\ \sin x&=x-\frac{1}{3 !} x^{3}+\cdots+(-1)^{n-1} \frac{x^{2 n-1}}{(2 n-1) !}+o\left(x^{2 n}\right) \\ \cos x&=1-\frac{1}{2 !} x^{2}+\cdots+(-1)^{n-1} \frac{x^{2 n}}{(2 n) !}+o\left(x^{2 n-1}\right) \\ \ln (1+x)&=x-\frac{1}{2} x^{2}+\frac{1}{3} x^{3}-\cdots+(-1)^{n-1} \frac{x^{n}}{n}+o\left(x^{n}\right) \\ (1+x)^{m}&=1+m x+\frac{m(m-1)}{2 !} x^{2}+\cdots+\frac{m(m-1) \cdots(m-n+1)}{n !} x^{n}+o\left(x^{n}\right) \\ \frac{1}{1-x}&=1+x+x^{2}+\cdots+x^{n}+o\left(x^{n}\right)\end{aligned}$$

基本导数与微分表

$$\begin{array}{c|c} \text { 导数公式 } & \text { 微分公式 } \\ \hline(C)^{\prime} = 0 & d C = 0 \\ \left(x^{\mu}\right)^{\prime} = \mu x^{\mu-1} & d\left(x^{\mu}\right) = \mu x^{\mu-1} d x \\ \left(a^{x}\right)^{\prime} = a^{x} \cdot \ln a & d\left(a^{x}\right) = a^{x} \cdot \ln x d x \\ \left(e^{x}\right)^{\prime} = e^{x} & d\left(e^{x}\right) = e^{x} d x \\ \left(\log _{a} x\right)^{\prime} = \frac{1}{x \ln a} & d\left(\log _{a} x\right) = \frac{1}{x \ln a} d x \\ (\ln x)^{\prime} = \frac{1}{x} & d(\ln x) = \frac{1}{x} d x \\ (\sin x)^{\prime} = \cos x & d(\sin x) = \cos x d x \\ (\cos x)^{\prime} = -\sin x & d(\cos x) = -\sin x d x \\ (\tan x)^{\prime} = \sec ^{2} x & d(\tan x) = \sec { }^{2} x d x\\ (\cot x)^{\prime}=-\csc ^{2} x & d(\cot x)=-\csc ^{2} x d x \\ (\sec x)^{\prime}=\sec x \cdot \tan x & d(\sec x)=\sec x \cdot \tan x d x \\ (\csc x)^{\prime}=-\csc x \cdot \cot x & d(\csc x)=-\csc x \cdot \cot x d x \\ (\arcsin x)^{\prime}=\frac{1}{\sqrt{1-x^{2}}} & d(\arcsin x)=\frac{1}{\sqrt{1-x^{2}}} d x \\ (\arccos x)^{\prime}=-\frac{1}{\sqrt{1-x^{2}}} & d(\arccos x)=-\frac{1}{\sqrt{1-x^{2}}} d x \\ (\arctan x)^{\prime}=\frac{1}{1+x^{2}} & d(\arctan x)=\frac{1}{1+x^{2}} d x \\ (\operatorname{arccot} x)^{\prime}=-\frac{1}{1+x^{2}} & d(\operatorname{arccot} x)=-\frac{1}{1+x^{2}} d x \end{array}$$

三角函数公式表

$$\begin{array}{c|c|c|c} 倒数关系 & 商的关系 & 平方关系 & 万能公式 \\ \hline \tan A \cot A =1 & \frac{\sin A}{\cos A} =\tan A=\frac{\sec A}{\csc A} & \sin^2 A +\cos^2 A =1&\sin A=\frac{2\tan(A/2)}{1+\tan2(A/2)}\\ \sin A \csc A =1 & \frac{\cos A}{\sin A} =\cot A=\frac{\csc A}{\sec A} & 1+\tan^2 A =\sec^2 A&\cos A=\frac{1-\tan2(A/2)}{1+\tan2(A/2)}\\ \cos A \sec A = 1 && 1+\cot^2 A =\csc^2 A&\tan A=\frac{2\tan(A/2)}{1-\tan2(A/2)}\\ \end{array}$$ $$\begin{array}{c|c|c} 两角和公式 & 半角公式 & 倍角公式 \\ \hline \sin (A+B) = \sin A \cos B+\cos A \sin B & \sin \left(\frac{A}{2}\right) = \sqrt{\frac{1-\cos A}{2}}&\tan 2 A = \frac{2 \tan A}{1-\tan ^{2} A} \\ \sin (A-B) = \sin A \cos B-\cos A \sin B & \cos \left(\frac{A}{2}\right) = \sqrt{\frac{1+\cos A}{2}}&\sin 2 A = 2 \sin A \cdot \cos A \\ \cos (A+B) = \cos A \cos B-\sin A \sin B & \cot \left(\frac{A}{2}\right) = \sqrt{\frac{1+\cos A}{1-\cos A}}&\cos 2 A = \cos ^{2} A-\sin ^{2} A \\ \cos (A-B) = \cos A \cos B+\sin A \sin B & \tan \left(\frac{A}{2}\right) = \sqrt{\frac{1-\cos A}{1+\cos A}}&\quad\quad= 2 \cos ^{2} A-1 \\ \tan (A+B) = \frac{\tan A+\tan B}{1-\tan A \tan B} & \quad\qquad= \frac{1-\cos A}{\sin A}&\quad\quad= 1-2 \sin ^{2} A\\ \tan (A-B) = \frac{\tan A-\tan B}{1+\tan A \tan B} & \quad\qquad= \frac{\sin A}{1+\cos A}&\sin 3 A = 3 \sin A-4(\sin A)^{3} \\ \cot (A+B) = \frac{\cot A \cot B-1}{\cot B+\cot A}&&\cos 3 A = 4(\cos A)^{3}-3 \cos A \\ \cot (A-B) = \frac{\cot A \cot B+1}{\cot B-\cot A}&&\tan 3 A = \tan A \cdot \tan (\frac{\pi}{3}+A) \cdot \tan (\frac{\pi}{3}-A) \end{array}$$ $$\begin{array}{c|c} 和差化积 & 积化和差 \\ \hline \sin A+\sin B = 2 \sin \frac{A+B}{2} \cos \frac{A-B}{2} &\sin A \cos B = \frac{1}{2}[\sin (A+B)+\sin (A-B)] \\ \sin A-\sin B = 2 \cos \frac{A+B}{2} \sin \frac{A-B}{2} &\sin A \sin B = \frac{1}{2}[\cos (A-B)-\cos (A+B)] \\ \cos A+\cos B = 2 \cos \frac{A+B}{2} \cos \frac{A-B}{2} &\cos A \cos B = \frac{1}{2}[\cos (A-B)+\cos (A+B)] \\ \cos A-\cos B = -2 \sin \frac{A+B}{2} \sin \frac{A-B}{2} &\cos A \sin B = \frac{1}{2}[\sin (A+B)-\sin (A-B)]\\ \tan A+\tan B = \frac{\sin (A+B)}{\cos A \cos B} \end{array}$$

常用高阶导数公式

1. $\left(a^{x}\right)^{(n)}=a^{x} \ln ^{n} a \quad(a>0) \quad ; \quad\left(e^{x}\right)^{(n)}=e^{x}$

2. $(\sin k x)^{(n)}=k^{n} \sin \left(k x+n \cdot \frac{\pi}{2}\right)$

3. $(\cos k x)^{(n)}=k^{n} \cos \left(k x+n \cdot \frac{\pi}{2}\right)$

4. $\left(x^{m}\right)^{(n)}=m(m-1) \cdots(m-n+1) x^{m-n}$

5. $(\ln x)^{(n)}=(-1)^{(n-1)} \frac{(n-1) !}{x^{n}}$

6. 莱布尼兹公式 (Leibniz’s) ：若$u(x)\,,v(x)$均$n$阶可导，则

   $$(uv)^{(n)}=\sum\limits_{i={0}}^{n}c_{n}^{i}u^{(i)}v^{(n-i)}$$

   其中$u^{(0)}=u$，$v^{(0)}=v$

Reduction Formulas for Power of Trigonometric Functions

$$\begin{align} &\int \sin ^{n} x d x=-\frac{\sin ^{n-1} x \cos x}{n}+\frac{n-1}{n} \int \sin ^{n-2} x d x\\ &\int \cos ^{n} x d x=\frac{\cos ^{n-1} x \sin x}{n}+\frac{n-1}{n} \int \cos ^{n-2} x d x\\ &\int \tan ^{n} x d x=\frac{\tan ^{n-1} x}{n-1}-\int \tan ^{n-2} x d x, n \neq 1\\ &\int \sec ^{n} x d x=\frac{\sec ^{n-2} x \tan x}{n-1}+\frac{n-2}{n-1} \int \sec ^{n-2} x d x, n \neq 1 \end{align}$$

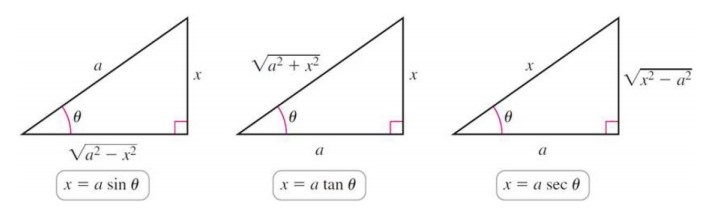
三角函数替换