【笔记】高等数学复习笔记-随机过程

基于 ChiuFai WONG 教授的随机过程课件的笔记；

结合应坚刚教授的随机分析讲义；

程士宏教授测度论与概率论基础进行整理；

对于部分基础多有忽略，主要用于知识点查找；

1. 概率论预备知识

1.1 集合的运算

$$\begin{array}{l}A \cup B \stackrel{\text { def }}{=}\{x: x \in A \text { 或 } x \in B\}, \\ A \cap B \stackrel{\text { def }}{=}\{x: x \in A \text { 且 } x \in B\}, \\ A \backslash B \stackrel{\text { def }}{=}\{x: x \in A \text { 且 } x \notin B\}, \\ A \Delta B \stackrel{\text { def }}{=}(A \backslash B) \bigcup(B \backslash A)\end{array}$$

分别称为集合 A 和 B 的并, 交, 差和对称差. 如 $B \subset A$ , 则 $A \backslash B$ 也称为 A 和 B 的真差.

1.2 单调序列

设 $\left\{A_{n}, n=1,2, \cdots\right\}$ 是一个集合序列. 如果对每个 $n=1,2, \cdots$ , 有

$$A_{n} \subset A_{n+1}$$

则称 $A_{n}$ 为非降的, 记为 $A_{n} \uparrow$ , 并把集合 $\lim_{n \rightarrow \infty} A_{n} \stackrel{ def }{=} \bigcup_{n=1}^{\infty} A_{n} $ 叫做它的极限;

如果对每个 $n=1,2, \cdots$ , 有

$$A_{n} \supset A_{n+1}$$

则称 $A_{n}$ 为非增的, 记为 $A_{n} \downarrow$ , 并称 $\lim_{n \rightarrow \infty} A_{n} \stackrel{ def }{=} \bigcap_{n=1}^{\infty} A_{n}$ 为它的极限. 非降或非增的集合序列统称为单调序列. 因此, 单调集合序列总有极限.

对于任意给定的一个集合序列 $\left\{A_{n}, n=1,2, \cdots\right\} $ , 集合序列非降和非增分别有极限

$$\liminf _{n \rightarrow \infty} A_{n}=\bigcup_{n=1}^{\infty} \bigcap_{k=n}^{\infty} A_{k} \qquad\text{和}\qquad\limsup _{n \rightarrow \infty} A_{n}=\bigcap_{n=1}^{\infty} \bigcup_{k=n}^{\infty} A_{k}$$

注意第二个运算符的范围是从 n 到 $\infty$ ，因此左边是非减右侧是非增

我们将把 $\liminf _{n \rightarrow \infty} A_{n}$ 和 $\lim _{n \rightarrow \infty} \sup A_{n}$ 分别叫做 $\left\{A_{n}, n=1,2, \cdots\right\}$ 的下极限和上极限.

1.3 集合系

以空间 X 中的一些集合为元素组成的集合成为 X 上的集合系，一般用花体字母来表示。

• $\pi$ 系：如果 X 上的非空集合系 $\mathscr{P}$ 对交是运算是封闭的，即

  $$A,B\in\mathscr{P}\Rightarrow A\bigcap B\in \mathscr{P}$$

  则称 $\mathscr{P}$ 为 $\pi$ 系

• 半环：满足 $\pi$ 系要求的基础上，对任意的 $A,B\in\mathscr{Q}$ 且 $A\supset B$，存在有限个两两不相交的 $\{C_k\in\mathscr{Q},k=1,…,n\}$ 使得

  $$A\backslash B=\bigcup_{k=1}^nC_k$$

• 环：如果 X 上的非空集合系 $\mathscr{R}$ 对并和差是运算是封闭的，则称 $\mathscr{R}$ 为 环

• 域：满足 $\pi$ 系要求的基础上

  $$X\in\mathscr{A};\quad A\in\mathscr{A}\Rightarrow A^c\in\mathscr{A}$$

• $\lambda$ 系：集合系 $\mathscr{L}$ 称为 $\lambda$ 系，如果它满足下列条件

  $$\begin{array}{l}X \in \mathscr{L} ; \\ A, B \in \mathscr{L} \text { 且 } A \supset B \Longrightarrow A \backslash B \in \mathscr{L}\\ A_{n} \in \mathscr{L} \text { 且 } A_{n} \uparrow \Longrightarrow \bigcup_{n=1}^{\infty} A_{n} \in \mathscr{L}\end{array}$$

• $\sigma$ 域：集合系 $\mathscr{F}$ 称为 $\sigma$ 域，如果它满足下列条件

  $$\begin{array}{l}X \in \mathscr{F} ; \\ A \in \mathscr{F} \Longrightarrow A^{c} \in \mathscr{F} \\ A_{n} \in \mathscr{F}, n=1,2, \cdots \Longrightarrow \bigcup_{n=1}^{\infty} A_{n} \in \mathscr{T}\end{array}$$

• Borel 集合系：$\mathscr{O}_R$ 为 $R$ 中开集组成的集合系

  $$\mathscr{B}\stackrel{ def }{=}\sigma(\mathscr{O})$$

1.4 事件域与信息

一个随机现象可能出现的所有结果称为样本空间 $\Omega$，$\mathscr{F}$ 是 $\Omega$ 的子集组成的集合，如果满足

1. $\emptyset, \Omega \in \mathscr{F}$
2. 如果 $A \in \mathscr{F}$, 则 $A^{c} \in \mathscr{F}$
3. 如果 $A_{n} \in \mathscr{F}, n \geq 1$ , 则 $\bigcup_{n} A_{n} \in \mathscr{F}$

则可称 $\mathscr{F}$ 为一个事件域，属于由 $\Omega$ 生成的 $\sigma$ 域 $\sigma(\Omega)$，而 $(\Omega,\mathscr{F},\mathbb{P})$ 是一个概率空间

2. 条件期望

2.1 期望和数字特征

连续性或者单调收敛定理：如果 $\xi_n$ 是非负递增的随机序列，那么

$$\mathbb{E}[\lim_n\xi_n]=\lim_n\mathbb{E}[\xi_n]$$

期望是随机变量的一个数字特征, 或者说是分布的数字特征, 表示平均. 这是最有用的, 它是使得函数 $f(x)=\mathbb{E}\left[(\xi-x)^{2}\right]$ 达到最小值的地方, 通常两个随机变量 $\xi, \eta$ 的均方距离定义为

$$\sqrt{\mathbb{E}[(\xi-\eta)^2]}$$

那么期望是实数空间中离 $\xi$ 的均方距离最近的数字. 实数空间是关于最少信息 $\{\empty,\Omega\}$ 可测的随机变量全体.

2.2 条件期望的直观

让我们用 Hilbert 空间的眼光看条件期望的问题, 我们已经有一个 Hilbert 空间 $ L^{2}(\Omega, \mathscr{F}, \mathbb{P}) $ , 关于部分信息 $ \mathscr{G} $ 可测的平方可积随机变量全体 $ L^{2}(\Omega, \mathscr{G}, \mathbb{P})$ 是 $ L^{2}(\Omega, \mathscr{F}, \mathbb{P}) $ 的闭子空间.

空间 $ L^{2}(\Omega, \mathscr{G}, \mathbb{P})$ 中距离 $\xi$ 最近的那个随机变量记为 $\mathbb{E}[\xi|\mathscr{G}]=\eta$ ，等价于说 $\eta$ 是 $\xi$ 在子空间上的正交投影，即 $\xi-\eta$ 与子空间垂直或者说正交，对于任何 $\zeta\in L^{2}(\Omega, \mathscr{G}, \mathbb{P})$ 有

$$\mathbb{E}[(\xi-\eta) \zeta]=0$$

2.3 条件期望的性质

1. 条件期望是线性算子

2. $\mathbb{E}[\xi \mid\{\emptyset, \Omega\}]=\mathbb{E}[\xi]$

3. 如果 $\xi$ 是 $\mathscr{G}$ 可测的, 那么 $\mathbb{E}[\xi \mid \mathscr{G}]=\xi$ . 这是因为投影算子在闭子空间自身上是恒等算子.

4. 条件期望有保正性: 如果 $\xi \geq 0$ a.s., 那么 $\mathbb{E}[\xi \mid \mathscr{G}] \geq 0$ a.s. 事实上, 由定义的第二条推出, 对任何 $A \in \mathscr{G}$ 有 $\mathbb{E}[\mathbb{E}[\xi \mid \mathscr{G}] ; A] \geq 0$, 因此 $\mathbb{E}[\xi \mid \mathscr{G}] \geq 0$.

5. 塔性 (相容性): 如果 $\mathscr{G}_{1} \subset \mathscr{G}_{2}$ 是两个子事件域, 那么

   $$\mathbb{E}\left[\mathbb{E}\left[\xi \mid \mathscr{G}_{2}\right] \mid \mathscr{G}_{1}\right]=\mathbb{E}\left[\xi \mid \mathscr{G}_{1}\right]=\mathbb{E}\left[\mathbb{E}\left[\xi \mid \mathscr{G}_{1}\right] \mid \mathscr{G}_{2}\right]$$

   如果 $\xi$ 在大的子空间上投影然后再投影到小的子空间上，等于它自己投影到小的子空间上

6. 如果 $\eta$ 是 $ \mathscr{G}$ 可测的随机变量, 那么

   $$\mathbb{E}[\xi \eta \mid \mathscr{G}]=\eta \mathbb{E}[\xi \mid \mathscr{G}]$$

7. 如果 $ \xi $ 与 $ \mathscr{G}$ 独立, 那么 $ \mathbb{E}[\xi \mid \mathscr{G}]=\mathbb{E} \xi$. 也就是说, $ \mathscr{G} $ 代表的信息对于预测 $ \xi $ 没有任何作用.

3. Discrete Markov Chain

• P denote the one-step transition matrix of probabilities
• A state $i$ is said to be absorbing if once entered they are never left
• the n-step transition probabilities ,$P_{i,j}^n$ to be the probability that a process in state i will be in state j after n additional transitions.
• Two states that communicate are said to be in the same class.
• $f_{i,j}^n$ to be the probability that, starting in i, the first transition into j occurs at time n.
• State i is said to be recurrent if $f_{i,i}=1$ and transient if $f_{i,i}<1$
• State i is said to be recurrent if $\sum_{n=0}^{\infty} P_{i, i}^{n}=\infty$ and transient if $\sum_{n=0}^{\infty} P_{i, i}^{n}<\infty$
• $P_{i, j}^{n}=f_{i, j}^{n}+f_{i, j}^{n-1} P_{j, j}^{1}+\cdots+f_{i, j}^{1} P_{i, i}^{n-1} \quad n \geq 1$

Theorem 1

Let $P_{i, j}(z)=\sum_{n=0}^{\infty} P_{i, j}^{n} z^{n}$ be the probability generating function of number of transition entering state $j$ starting from state $i$ and let $\delta_{i, j}=\left\{\begin{array}{cc}1 & \text { if } i=j \ 0 & \text { otherwise. }\end{array}\right.$ Then $P_{i, j}(z)=\delta_{i, j}+f_{i, j}(z) P_{j, j}(z)$. In particular,

$$P_{i, i}(z)=\frac{1}{1-f_{i, i}(z)}$$

Theorem 2

Let $T$ denote the set of all transient states. If $j$ is recurrent, then the set of probabilities $\left\{f_{i, j}, i \in T\right\}$ satisfies

$$f_{i, j}=\sum_{k \in T} P_{i, k} f_{k, j}+\sum_{k \in R_{j}} P_{i, k}, \quad i \in T,$$

where $R_{j}$ denotes the set of recurrence states communicating with $j$.

Theorem 3

Assuming that successive plays of the game are independent, what is the probability that, starting with $i$ units, the gambler’s fortune will reach $N$ before reaching 0?

$$P_{i}=\left\{\begin{array}{cc} \frac{1-(q / p)^{i}}{1-(q / p)^{N}}, & \text { if } p \neq \frac{1}{2} \\ \frac{i}{N}, & \text { if } p=\frac{1}{2} \end{array}\right.$$

The expected number of bets that the gambler starting at $k, 0 < k < N$, will reach $0$ or $N$ is

$$m_{k}=\left\{\begin{array}{cl} \frac{1}{2 p-1}\left[N \frac{1-(q / p)^{k}}{1-(q / p)^{N}}-k\right] & \text { if } p \neq \frac{1}{2} \\ N k-k^{2} & \text { if } p=\frac{1}{2} \end{array}\right.$$

• let $m_{i,j}$ denote the expected number of visits in state $j$, given that

  it starts in state $i$.

• $m_{i, j}=\delta_{i, j}+\sum_{k} P_{i, k} m_{k, j}$, $M=I_{t}+P_{T} M\to M=\left(I_{t}-P_{T}\right)^{-1}$

• $f_{i, j}=\frac{m_{i, j}-\delta_{i, j}}{m_{j, j}}$

• A state with period 1 is said to be aperiodic

• $\mu_{i,j}$ denote the expected number of transition need to return state $i$. That is, $\mu_{i,i}=\sum_{n=1}^\infty nf_{i,i}^n$

• If the expected recurrence time is finite then this is called positive-recurrent; if the expected recurrence time is infinite then this is called null recurrent. Positive recurrent, aperiodic states are called ergodic.

Stirling’s approximation

for $n$ large

$$n!\approx\sqrt{2\pi n}(\frac n e)^n$$

1-dimensional Simple Random Walk

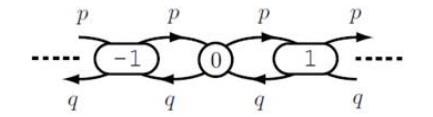
• The chain is recurrent when $p=\frac12$ and transient if $p\ne\frac12$

Because $f_{0,1}(z)=pz+(qz)f_{0,1}(z)f_{-1,0}(z)=pz+(qz)f_{0,1}(z)^2$

we obtain

$$f_{0,1}(z)=\frac{1-\sqrt{1-4pqz^2}}{2qz}=p z+\cdots+\frac{(2 n-2) !}{n !(n-1) !} p^{n} q^{n-1} z^{2 n-1}+\cdots$$

So $p_{2n-1}=\frac{(2 n-2) !}{n !(n-1) !} p^{n} q^{n-1}$. As the same $q_{2n-1}=\frac{(2 n-2) !}{n !(n-1) !} p^{n-1} q^{n}$.

Then

$$f_{0,0}(z)=(p z) f_{1,0}(z)+(q z) f_{-1,0}(z)=(p z) f_{0,-1}(z)+(q z) f_{0,1}(z)=1-\sqrt{1-4 p q z^{2}}$$

And

$$f_{0,0}=f_{0,0}(1)=1-\sqrt{1-4 p q}=1-\sqrt{(p+q)^{2}-4 p q}=1-\sqrt{(p-q)^{2}}=1-|p-q|$$

if $p=q$

$$\mu_{i,i}=f'_{0,0}(1)=\frac z{\sqrt{1-z^2}}\bigg|_{z=1}=\infty$$

• $\pi_j=\sum_i\pi_jP_{i,j}$ is called stationary probability.
• $\pi_j=\lim_{n\to\infty}P_{i,j}^n$ and $\pi P=\pi\to\pi(P-I)=0$

For an irreducible Markov chain, suppose state $i$ has period $d$

$$\lim_{n\to\infty}P_{i,i}^{nd}=\frac d{\mu_{i,i}}=d\pi_i$$

4. Poisson Process

$$P(N(t+s)-N(s)=n)=e^{-\lambda t} \frac{(\lambda t)^{n}}{n !}, \quad n=0,1, \cdots$$

• $\lambda$ is called the rate of the process

• $\{T_n,n=1,2,…\}$ is called the sequence of interarrival times.

  $$\begin{aligned} P\left(T_{2}>t \mid T_{1}=s\right) &=P\left(0 \text { events in }(s, s+t] \mid T_{1}=s\right) \\ &=P(0 \text { events in }(s, s+t]) \\ &=e^{-\lambda t} \end{aligned}$$

  $T_1$ has an exponential distribution with mean $1/\lambda$.

• $S_n=\sum_{i=1}^nT_i,n\ge 1$ called the waiting time until the nth event

  $$M_{S_{n}}(t)=E\left[e^{t\left(T_{1}+\cdots+T_{n}\right)}\right]=E\left[e^{t T_{1}}\right] \cdots E\left[e^{t T_{n}}\right]=\left(\frac{\lambda}{\lambda-t}\right)^{n} \quad \text { for } t<\lambda$$

  $S_n$ has a gamma distribution with parameters n and $\lambda$, and $P\left(S_{n} \leq t\right)=P(N(t) \geq n)$

5. Brownian Motion

Define

$$\Delta x=\sigma \sqrt{\Delta t}, \quad \text { and } \quad p=\frac{1}{2}\left(1+\frac{\mu}{\sigma} \sqrt{\Delta t}\right)$$

the position at time t, is

$$W_{n}(t)=\sigma \sqrt{\Delta t}\left(X_{1}+\cdots+X_{n}\right)$$

Now

$$E\left[X_{i}\right]=1(p)-1(1-p)=2 p-1=\frac{\mu}{\sigma} \sqrt{\Delta t} \quad \text { and } \quad \operatorname{Var}\left[X_{i}\right]=E\left[X_{i}^{2}\right]-E\left[X_{i}\right]^{2}=1-(2 p-1)^{2}$$

Then

$$E[W_n(t)]=\mu t\qquad Var(W_n(t))=\sigma^2t(1-(2p-1)^2)$$

Theorem 1

Set $W\left(t_{1}\right)=x_{1}, W\left(t_{2}\right)=x_{2}, \cdots, W\left(t_{m}\right)=x_{m}$

$$f(x_1,x_2,\cdots,x_m)=\frac{1}{(2 \pi)^{m / 2} \sigma^{m} \sqrt{t_{1}\left(t_{2}-t_{1}\right) \cdots\left(t_{m}-t_{m-1}\right)}} e^{-\frac{1}{2 \sigma^{2}}\left[\frac{\left.\left(x_{1}-\mu_{1}\right)^{2}\right|}{t_{1}}+\frac{\left(\left(x_{2}-x_{1}\right)-\mu\left(t_{2}-t_{1}\right)\right)^{2}}{t_{2}-t_{1}}+\cdots+\frac{\left(\left(x_{m}-x_{m-1}\right)-\mu\left(t_{m}-t_{m-1}\right)\right)^{2}}{t_{m}-t_{m-1}}\right]}$$

Theorem 2

The probability of $W(t)+x$ starting at x will hit A before B where $B\le x\le A$ is

$$P(\text{up to A beforce down to B | starting at x})=\left\{\begin{array}{cl} \frac{1-e^{-2 \mu(x-B) / \sigma^{2}}}{1-e^{-2 \mu(A-B) / \sigma^{2}},} & \text { if } \mu \neq 0 \\ \frac{x-B}{A-B}, & \text { if } \mu=0 \end{array}\right.$$

If $\mu>0$, by letting $A\to\infty$,

$$P(\text{never goes down to B | starting at x})=\lim _{A \rightarrow \infty} \frac{1-e^{-2 \mu(x-B) / \sigma^{2}}}{1-e^{-2 \mu(A-B) / \sigma^{2}}}=1-e^{-\frac{2 \mu(x-B)}{\sigma^{2}}}$$

Theorem 3

Define the stopping time T by $T=min\{t:W(t)=A\quad or\quad W(t)=B\}$

$$E[T]=\left\{\begin{array}{cl} \frac{(A-x)(x-B)}{\sigma^{2}} & \text { if } \mu=0 \\ \frac{(A-x)\left(e^{2 \mu(x-B) / \sigma^{2}}-1\right)+(x-B)\left(e^{-2 \mu(A-x) / \sigma^{2}}-1\right)}{\mu\left(e^{2 \mu(x-B) / \sigma^{2}}-e^{-2 \mu(A-x) / \sigma^{2}}\right)} & \text { if } \mu \neq 0 \end{array}\right.$$

Let $T_A$ denote the first time W(t) is equal to A, by setting $B\to\infty$

$$E[T_A]=\frac{A-x}{\mu}+\lim _{x - B \rightarrow \infty} \frac{e^{-2 \mu(A-x) / \sigma^{2}}-1}{\mu e^{2 \mu(x-B) / \sigma^{2}}\left(2 \mu / \sigma^{2}\right)}=\frac{A-x}{\mu}$$

Theorem 4

$$\begin{aligned} &P\left(T_{A} \leq t\right)=P\left(\max _{0 \leq s \leq t} W(s) \geq A\right)=e^{\frac{2 \mu(A-x)}{\sigma^{2}}}\left(1-N\left(\frac{A-x+\mu t}{\sigma \sqrt{t}}\right)\right)+\left(1-N\left(\frac{A-x-\mu t}{\sigma \sqrt{t}}\right)\right) \\ &P\left(T_{B} \leq t\right)=P\left(\min _{0 \leq s \leq t} W(s) \leq B\right)=e^{-\frac{2 \mu(x-B)}{\sigma^{2}}}\left(1-N\left(\frac{x-B-\mu t}{\sigma \sqrt{t}}\right)\right)+\left(1-N\left(\frac{x-B+\mu t}{\sigma \sqrt{t}}\right)\right) \end{aligned}$$

6. Geometric Brownian Motion

$$S(t)=S(0)e^{W(t)}=S(0)e^{\sigma Z(t)+\mu t}$$

$ln(S(t)/S(0))$ is normally distributed with parameters $(\mu t,\sigma^2t)$.Then $S(t)/S(0)$ has a lognormal distribution with parameters $(\mu t,\sigma^2 t)$E

$$E[S(t)]=S(0)e^{(\mu+\sigma^2/2)t}$$

Theorem 1

The covariance of $S(t_1)$ and $S(t_2)$, for $t_1<t_2$

Let $Q_{1}=S\left(t_{1}\right) / S(0)=e^{\mu t_{1}+\sigma Z\left(t_{1}\right)}$ and $Q_{2}=S\left(t_{2}\right) / S\left(t_{1}\right)=e^{\mu\left(t_{2}-t_{1}\right)+\sigma Z\left(t_{2}-t_{1}\right)}$

$$\begin{aligned} E\left[S\left(t_{1}\right) S\left(t_{2}\right)\right] &=S(0)^{2} E\left[Q_{1}^{2} Q_{2}\right] \\ &=S(0)^{2} E\left[Q_{1}^{2}\right] E\left[Q_{2}\right] \\ &=S(0)^{2} e^{2 \mu t_{1}+2 \sigma^{2} t_{1}} e^{\mu\left(t_{2}-t_{1}\right)+0.5 \sigma^{2}\left(t_{2}-t_{1}\right)} \\ &=S(0)^{2} e^{\mu\left(t_{2}+t_{1}\right)+\sigma^{2}\left(1.5 t_{1}+0.5 t_{2}\right)} \end{aligned}$$ $$\begin{aligned} Cov\left(S\left(t_{1}\right), S\left(t_{2}\right)\right)&=E\left[S\left(t_{1}\right) S\left(t_{2}\right)\right]-E\left[S\left(t_{1}\right) \right]E\left[S\left(t_{2}\right) \right]\\ &=S(0)^{2}\left(e^{\mu\left(t_{1}+t_{2}\right)+\sigma^{2}\left(1.5 t_{1}+0.5 t_{2}\right)}-e^{\mu\left(t_{1}+t_{2}\right)+0.5 \sigma^{2}\left(t_{1}+t_{2}\right)}\right)\\ &=S(0)^{2} e^{\left(\mu+0.5 \sigma^{2}\right)\left(t_{1}+t_{2}\right)}\left(e^{\sigma^{2} t_{1}}-1\right) \end{aligned}$$ $$\begin{aligned} \rho_{S\left(t_{1}\right), S\left(t_{2}\right)}&=\frac{\operatorname{Cov}\left(S\left(t_{1}\right), S\left(t_{2}\right)\right)}{\sigma_{S\left(t_{1}\right)} \sigma_{S\left(h_{2}\right)}}\\ &=\frac{S(0)^{2} e^{\left(\mu+0.5 \sigma^{2}\right)\left(\left(_{1}+t_{2}\right)\right.}\left(e^{\sigma^{2} t_{1}}-1\right)}{\sqrt{S(0)^{2} e^{2\left(\mu+0.5 \sigma^{2}\right) x_{1}}\left(e^{\sigma^{2} t_{1}}-1\right) S(0)^{2} e^{2\left(\mu+0.5 \sigma^{2}\right) r_{2}}\left(e^{\sigma^{2} t_{2}}-1\right)}}\\ &=\sqrt{\frac{e^{\sigma^{2} t_{1}}-1}{e^{\sigma^{2} t_{2}}-1}} \end{aligned}$$

Suppose $S_1\left(t\right)=S_1(0)e^{\mu_1 t+\sigma_1 Z_2\left(t\right)}$ and $S_2\left(t\right)=S_2(0)e^{\mu_2 t+\sigma_2 Z_2\left(t\right)}$

$$Cov\left(S_{1}(t), S_{2}(t)\right)=S_{1}(0) S_{2}(0) e^{\left(\mu_{1}+\mu_{2}\right) t+\frac{1}{2}\left(\sigma_{1}^{2}+\sigma_{2}^{2}\right) t}\left(e^{\rho \sigma_{1} \sigma_{2} t}-1\right)$$ $$\rho_{S_{1}(t), S_{2}(t)}=\frac{e^{\rho \sigma_{1} \sigma_{2} t}-1}{\sqrt{\left(e^{\rho \sigma_{1}^{2} t}-1\right)\left(e^{\rho \sigma_{2}^{2} t}-1\right)}}$$

7. Price jump

$S_J(t)$ denote the stock price (with jump) at time t

$$S_J(t)=S(t)\prod_{i=1}^{N(t)} J_{i},\quad t\ge 0$$ $$\begin{aligned} E\left[\prod_{i=1}^{N(t)} J_{i}\right] &=\sum_{n=0}^{\infty} E\left[\prod_{i=1}^{N(t)} J_{i} \mid N(t)=n\right] P(N(t)=n) \\ &=\sum_{n=0}^{\infty}(E[J])^{n} \frac{e^{-\lambda t}(\lambda t)^{n}}{n !} \\ &=e^{-\lambda t} \sum_{n=0}^{\infty} \frac{(\lambda E[J] t)^{n}}{n !} \\ &=e^{-\lambda t(1-E[J])} \end{aligned}$$ $$E\left[S_{J}(t)\right]=E\left[S(t) \prod_{i=1}^{N(t)} J_{i}\right] \stackrel{\text { independence }}{=} E[S(t)] E\left[\prod_{i=1}^{N(t)} J_{i}\right]=S(0) e^{\left(\mu+\sigma^{2} / 2-\lambda(1-E[J]) r\right.}$$

Set $\mu=r-\sigma^2/2+\lambda(1-E[J])$

If the jumps $J_i$ have a lognormal distribution $X_i=ln(J_i),i\ge 1$ with mean $\mu_0$ and variance $\sigma_0^2$.The no-arbitrage cost of a European call option having strike price K and expiration time T is

$$e^{-r T} E\left[\left(S_{J}(T)-K\right)^{+}\right]=e^{-r T} E\left[\left(S(0) e^{W(T)} \prod_{i=1}^{N(T)} J_{i}-K\right)^{+}\right]=e^{-r T} E\left[\left(S(0) e^{W(T)+\sum_{i=1}^{N(T)} X_{i}}-K\right)^{+}\right]$$

eq to

$$\sum_{n=0}^\infty e^{-\lambda E[J]T}\frac{(\lambda E[J]T)^n}{n!}C(S(0),T,K,\sigma(n),r(n))$$

where

$$\sigma(n)=\sqrt{\sigma^{2}+\frac{n \sigma_{0}^{2}}{T}}, \quad E[J]=e^{\mu_{0}+\frac{\sigma_{0}^{2}}{2}} \quad \text { and } \quad r(n)=\mu+\sigma^{2} / 2+\lambda(1-E[J])+\frac{n \ln E[J]}{T}$$

A jump is called pure if the jump happens at a specific time

$$S_J(t)=S(t)U^{N_1(t)}D^{N_2(t)},\quad t\ge 0$$

where

$$N_1(t)\sim Poisson(\lambda p),N_2(t)\sim Poisson(\lambda (1-p))$$ $$E\left[S_{J}(t)\right]=E\left[S(t) U^{N_{1}(t)} D^{N_{2}(t)}\right]=E[S(t)] E\left[U^{N_{1}(t)}\right] E\left[D^{N_{2}(t)}\right]=S(0) e^{\left(\mu+\sigma^{2} / 2+\lambda p(U-1)+\lambda(1-p)(D-1)\right) t}$$

Under the above assumption, the no-arbitrage cost of a European call option having strike price K and expiration time T is given by

$$\sum_{m=0}^{\infty} \sum_{n=0}^{\infty} e^{-\lambda p T} \frac{(\lambda p T)^{m}}{m !} e^{-\lambda(1-p) T} \frac{(\lambda(1-p) T)^{n}}{n !} C\left(S(0) U^{m} D^{n}, T, K, \sigma, r\right)$$