基于吴恩达机器学习 - Machine Learning Specialization 课程的笔记第一部分；基础部分；

Course 1 : Supervised Machine Learning: Regression and Classification

In the first course of the Machine Learning Specialization, you will:

Build machine learning models in Python using popular machine learning libraries NumPy and scikit-learn.
Build and train supervised machine learning models for prediction and binary classification tasks, including linear regression and logistic regression

Week 1 : Introduction to Machine Learning

1. Introduction

1.1 监督学习 Supervised Learning

回归问题 - 连续输出
分类问题（支持向量机） - 离散输出

1.2 无监督学习 Unsupervised Learning

聚类算法 - 把个体聚类到不同的类或不同类型的组
- 谷歌新闻搜索非常多的新闻事件，自动地将同一主题的新闻事件聚类到一起
- 组织大型计算机集群，判断什么样的机器易于协同地工作，使数据中心工作得更高效
- 进行社交网络的分析，自动地将熟悉的人分在一起
- 通过检索消费者信息，自动地发现市场分类，并地把顾客划分到不同的细分市场中，更有效地在不同的细分市场一起进行销售产品
- 天文数据分析
鸡尾酒会问题 cocktail party problem - 将两个说话的声音区分开来

2. Linear Regression with One Variable

2.1 Model Representation

我们将要用来描述这个回归问题的标记如下:

$m$ 代表训练集中实例的数量
$x$ 代表特征/输入变量
$y$ 代表目标变量/输出变量
$\left( x,y \right)$ 代表训练集中的实例
$(x^{(i)},y^{(i)})$ 代表第$i$ 个观察实例
$h$ 代表学习算法的解决方案或函数也称为假设（hypothesis）
$\theta_{0}$ 和 $\theta_{1}$ 代表需要训练的参数（parameters）

因为只含有一个特征/输入变量，因此这样的问题叫作单变量线性回归问题

$h_\theta ( x )=\theta_{0} + \theta_{1}x$

2.2 Cost Function

我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数。即使得代价函数 $J$ 最小

$J \left( \theta_0, \theta_1 \right) = \frac{1}{2m}\sum\limits_{i=1}^m \left( h_{\theta}(x^{(i)})-y^{(i)} \right)^{2}$

此处 $\frac12$ 是为了在后面求导的时候能消去 2，方便运算

此处采用 Squared error cost function 是因为，对于大多数问题，特别是回归问题，都是一个合理的选择。还有其他的代价函数也能很好地发挥作用，但 Squared error cost function 是解决回归问题最常用的手段了。

【Python 代码】

def cost(X, y, theta):
    
    inner = np.power(((X * theta.T) - y), 2)
    return np.sum(inner) / (2 * len(X))

2.3 Gradient Descent Intuition

梯度下降算法为

$\theta_{j}:=\theta_{j}-\alpha \frac{\partial }{\partial \theta_{j}}J\left(\theta \right)$

在梯度下降法中，当我们接近局部最低点时，梯度下降法会自动采取更小的幅度，这是因为当我们接近局部最低点时，很显然在局部最低时导数等于零，所以当我们接近局部最低时，导数值会自动变得越来越小，所以梯度下降将自动采取较小的幅度，这就是梯度下降的做法。

其中 $\alpha$ 是学习率（learning rate），决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大。

如果 $\alpha$ 太小，更新可能会很慢，它会需要很多步才能到达全局最低点
如果 $\alpha$ 太大，梯度下降法可能会越过最低点，会导致无法收敛，甚至发散。

同时，当参数已经处于局部最低点时，梯度下降法将不会改变参数的值，这导致参数最终停留在局部最低而不是全局最优点。

显然，在梯度下降的过程中要考虑合适的学习率与初始值，才能得到好的结果

更深入的理解可以观看B站视频《图解机器学习的数学直觉》中，图解微积分 Jacobian 和 Jacobian matrix 的部分

2.4 Gradient Descent for Linear Regression

对我们之前的线性回归问题运用梯度下降法，关键在于求出代价函数的导数，即：

$\frac{\partial }{\partial \theta _{j}}J(\theta _{0},\theta _{1})=\frac{\partial }{\partial \theta _{j}}\frac{1}{2m}\sum\limits_{i=1}^{m}{\left( h_{\theta }(x^{(i)})-y^{(i)} \right)}^{2}$

$j=0$ 时：$\frac{\partial }{\partial \theta _{0}}J(\theta _{0},\theta _{1})=\frac{1}{m}\sum\limits_{i=1}^{m}{\left( h_{\theta }(x^{(i)})-y^{(i)} \right)}$
$j=1$ 时：$\frac{\partial }{\partial \theta _{1}}J(\theta _{0},\theta _{1})=\frac{1}{m}\sum\limits_{i=1}^{m}{\left( \left( h_{\theta }(x^{(i)})-y^{(i)} \right)\cdot x^{(i)} \right)}$

此处采用的是批量梯度下降 （batch gradient descent），即在梯度下降的每一步中，用到了所有的训练样本（$m$) 来进行函数优化

则算法改写成：

$\theta_{0}:=\theta_{0}-a\frac{1}{m}\sum\limits_{i=1}^{m}{ \left(h_{\theta }(x^{(i)})-y^{(i)} \right)}$ $\theta_{1}:=\theta_{1}-a\frac{1}{m}\sum\limits_{i=1}^{m}{\left( \left(h_{\theta }(x^{(i)})-y^{(i)} \right)\cdot x^{(i)} \right)}$

线性回归的代价函数都是凸函数（convex function），因此不用担心仅仅得到局部最优的结果。

注意，国内对凹凸函数的定义与国外相反，仅有经济学上是一致的，在这我们定义向下凸出的为凸函数。

【Python 代码】

def gradient(X, Y, theta, alpha, iters):
    
    parameters = int(theta.shape[1])
    cost = np.zeros(iters)

    for i in range(iters):
        error = X * theta.T - Y
        term = np.multiply(error, X)
        theta= theta - alpha / len(X) * np.sum(term,axis=0)
        cost[i] = computeCost(X, Y, theta)
    
    return theta, cost
# 在函数内赋值不会对 theta 做影响

【scikit-learn】

from sklearn import linear_model

model = linear_model.LinearRegression()
model.fit(X, Y)

x = np.array(X[:, 1].A1)
y = model.predict(X).flatten()

fig, ax = plt.subplots(figsize=(12,8))
ax.plot(x, y, 'r', label='Prediction')
ax.scatter(data.Population, data.Profit, label='Traning Data')
ax.legend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()

3. Linear Algebra Review

此部分由于过于基础可以参考线性代数单独的笔记进行学习

Week 2 : linear regression with multiple variables

4. Multivariate Linear Regression

4.1 Multiple Features

增添更多特征 $\left( x_{1},x_{2},…,x_{n} \right)$ 后，我们引入一系列新的注释：

$n$ 代表特征的数量
${x^{\left( i \right)}}$代表第 $i$ 个训练实例，是特征矩阵中的第$i$行，是一个向量（vector）
$x_{j}^{\left( i \right)}$代表特征矩阵中第 $i$ 行的第 $j$ 个特征，也就是第 $i$ 个训练实例的第 $j$ 个特征
支持多变量的假设 $h$ 表示为：$h_{\theta}( x )=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+…+\theta_{n}x_{n}$
因此公式可以简化为：$h_{\theta} ( x )=\theta^{T}X$

4.2 Gradient Descent for Multiple Variables

为了使得公式能够简化一些，引入$x_{0}=1$

多变量线性回归的批量梯度下降算法，当$n>=1$时，

$\theta_j:=\theta_j-a\frac{1}{m}\sum\limits_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})x_{j}^{(i)}$

【Python 代码】

# 画出拟合平面
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()
ax = Axes3D(fig)
X_ = np.arange(mins[0], maxs[0]+1, 1)
Y_ = np.arange(mins[1], maxs[1]+1, 1)
X_, Y_ = np.meshgrid(X_, Y_)
Z_ = theta[0] + theta[1] * X_ + theta[2] * Y_

# 手动设置角度
ax.view_init(elev=25, azim=125)

ax.set_xlabel('Size')
ax.set_ylabel('Bedrooms')
ax.set_zlabel('Price')

ax.plot_surface(X_, Y_, Z_, rstride=1, cstride=1, color='red')

ax.scatter(data_[:, 0], data_[:, 1], data_[:, 2])
plt.show()

4.3 Gradient Descent in Practice I - Feature Scaling

在我们面对多维特征问题的时候，我们需要保证这些特征都具有相近的尺度，这将帮助梯度下降算法更快地收敛

考虑到我们设定 $x_0=1$ , 因此我们希望变量的值都在 $[-1,1]$ 左右

如果不采用 Feature Scaling ，而直接进行计算，可能会进入如下图红色路径需要多次迭代才能收敛的状态

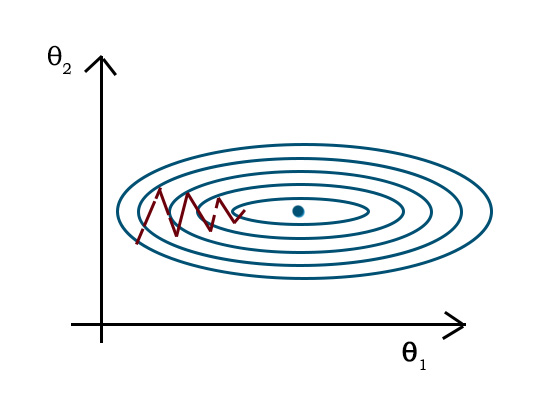
【Mean normalization】

我们在对数据进行处理的时候可以直接除一个数，或者是使用均值归一化

$x_n=\frac{x_n-\mu_n}{s_n}$

其中 $\mu_n$是平均值，$s_n$是标准差

【Python 代码】

data_norm = (data - data.mean()) / data.std()

# or

from sklearn.preprocessing import StandardScaler

data_norm = scaler.fit_transform(data)

# 参数转化为缩放前

def theta_transform(theta, means, stds):
    temp = means[:-1] * theta[1:] / stds[:-1]
    theta[0] = (theta[0] - np.sum(temp)) * stds[-1] + means[-1]
    theta[1:] = theta[1:] * stds[-1] / stds[:-1]
    return theta.reshape(1, -1)

4.4 Gradient Descent in Practice II - Learning Rate

梯度下降算法的每次迭代受到学习率的影响，如果学习率 $\alpha$ 过小，则达到收敛所需的迭代次数会非常高；如果学习率过 $\alpha$ 大，每次迭代可能不会减小代价函数，反而会越过局部最小值导致无法收敛。我们可以通过观察迭代次数与 $J(\theta)$ 的关系来判断学习率取值的好坏。

通常可以考虑尝试些学习率：$\alpha=…,0.01，0.03，0.1，0.3，1，3，10,…$

4.5 Features and Polynomial Regression

线性回归并不适用于所有数据，有时我们需要曲线来适应我们的数据，比如一个二次方模型：

$h_{\theta}( x )=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}^2$

4.6 Normal Equation

到目前为止，我们都在使用梯度下降算法，但是对于某些线性回归问题，Normal Equation 作为更好的解决方案可以一次性解出最优的值。

$\theta =\left( {X^T}X \right)^{-1}X^{T}y$

在使用这个方法的时候，Feature Scaling 可以不用做

梯度下降与正规方程的比较：

梯度下降	正规方程
需要选择学习率$\alpha$	不需要选择学习率$\alpha$
需要多次迭代	一次运算得出
当特征数量$n$大时也能较好适用	需要计算$\left( X^TX \right)^{-1}$ 如果特征数量n较大则运算代价大，因为矩阵逆的计算时间复杂度为$O\left( n^3 \right)$，通常来说当$n$小于10000 时还是可以接受的
适用于各种类型的模型	只适用于线性模型，不适合逻辑回归模型等其他模型

【推导过程】

$J\left( \theta \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}\left( h_{\theta}\left( x^{(i)} \right)-y^{(i)} \right)^{2}$ $h_{\theta}( x )=\theta^{T}X=\theta_{0}x_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+\cdots+\theta_{n}x_{n}$

将向量表达形式转为矩阵表达形式，则有

$\begin{aligned} J(\theta )&=\frac{1}{2}\left( X\theta -y\right)^{T}\left( X\theta -y \right)\\ &=\frac{1}{2}\left( \theta ^{T}X^T-y^{T} \right)\left(X\theta -y \right)\\ &=\frac{1}{2}\left( \theta ^{T}X^TX\theta -\theta^{T}X^Ty-y^{T}X\theta -y^{T}y \right) \end{aligned}$

接下来对$J(\theta )$偏导，需要用到以下几个矩阵的求导法则:

$\frac{dAB}{dB}=A^{T}$
$\frac{dX^{T}AX}{dX}=2AX$

所以有

$\begin{aligned} \frac{\partial J\left( \theta \right)}{\partial \theta }&=\frac{1}{2}\left(2X^TX\theta -X^Ty -(y^{T}X )^{T}-0 \right)\\ &=\frac{1}{2}\left(2X^TX\theta -X^Ty -X^Ty -0 \right)\\ &=X^TX\theta -X^Ty \end{aligned}$

当等式取 0 时，则有$\theta =\left( X^{T}X \right)^{-1}X^{T}y$

【python 代码】

def normalEqn(X, y):
    
   theta = np.linalg.inv(X.T@X)@X.T@y 

	#X.T@X等价于X.T.dot(X)
    
   return theta

Week 3: Logistic Regression

5. Classification and Representation

5.1 Classification

我们从二元的分类问题开始讨论，将因变量（dependent variable）可能属于的两个类分别称为负向类（negative class）和正向类（positive class），则因变量$y\in { 0,1 \\}$ ，其中 0 表示负向类，1 表示正向类。

如果我们要用线性回归算法来解决一个分类问题，那么假设函数的输出值可能远大于 1，或者远小于0，即使所有训练样本的标签 $y$ 都等于 0 或 1。所以我们在接下来的要研究的算法就叫做逻辑回归算法，这个算法的性质是：它的输出值永远在0到 1 之间。

5.2 Hypothesis Representation

根据线性回归模型我们只能预测连续的值，然而对于分类问题，我们需要输出0或1，我们可以预测：

当$h_\theta( x )>=0.5$时，预测 $y=1$
当$h_\theta( x )<0.5$时，预测 $y=0$

逻辑回归模型的假设函数是

$h_\theta ( x )=g\left(\theta^{T}X \right),\qquad g\left( z \right)=\frac{1}{1+e^{-z}}$

其中 $g$ 代表逻辑函数（logistic function）是一个常用的逻辑函数为S形函数（Sigmoid function）

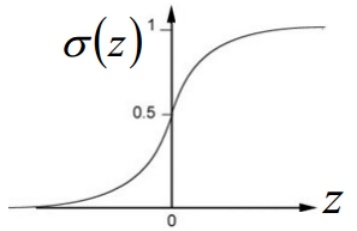
$h_\theta ( x )$的作用是，对于给定的输入变量，根据选择的参数计算输出变量为 1 的可能性（estimated probablity）即 $h_\theta ( x )=P\left( y=1|x;\theta \right)$

【python 代码】

1
2
3

def sigmoid(z):
    
   return 1 / (1 + np.exp(-z))

5.3 Decision Boundary

根据上面绘制出的 S 形函数图像，我们知道当

$z\geq0$ 时 $g(z)\geq0.5$，即 $\theta^{T}x>=0$ 时，预测 $y=1$
$z<0$ 时 $g(z)<0.5$，即 $\theta^{T}x<0$ 时，预测 $y=0$

逻辑回归实际上是以 $\theta^{T}=0$ 构成的函数为分界线，将预测为1的区域和预测为 0的区域分隔开。上为正，下为负。这条分界线就被成为决策边界（Decision Boundary）

【python 代码】

def predict(theta, X):
    
    probability = sigmoid(X @ theta.T)
    return [1 if x >= 0.5 else 0 for x in probability]

6. Logistic Regression Model

6.1 Cost Function

对于线性回归模型，我们定义的代价函数是所有模型误差的平方和。理论上来说，我们也可以对逻辑回归模型沿用这个定义，但是问题在于，当我们将 $h_\theta( x )=\frac{1}{1+e^{-\theta^{T}x}}$ 带入到这样定义了的代价函数中时，我们得到的代价函数将是一个非凸函数（non-convexfunction）。这意味着我们的代价函数有许多局部最小值，这将影响梯度下降算法寻找全局最小值。

我们重新定义逻辑回归的代价函数为

$J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}\text{Cost}\left( h_\theta\left( x^{(i)} \right),y^{(i)} \right)$ $\text{Cost}\left(h_{\theta}(x), y\right)=\left\{\begin{aligned}-\log \left(h_{\theta}(x)\right) & \text{ if } y=1 \\-\log \left(1-h_{\theta}(x)\right) & \text{ if } y=0 \end{aligned}\right.$

当实际的 $y=1$ 且 $h_\theta( x )$ 也为 1 时误差为 0
当 $y=1$ 但 $h_\theta( x )$ 不为1时误差随着 $h_\theta( x )$ 变小而变大
当实际的 $y=0$ 且 $h_\theta( x )$ 也为 0 时代价为 0
当 $y=0$ 但 $h_\theta( x )$ 不为 0 时误差随着 $h_\theta( x )$ 的变大而变大

简化如下：

$Cost\left( h_\theta( x ),y \right)=-y\times log\left( h_\theta( x ) \right)-(1-y)\times log\left( 1-h_\theta( x ) \right)$

【Python 代码】

def cost(theta, X, Y):
    
    first = Y * np.log(sigmoid(X@theta.T))
    second = (1 - Y) * np.log(1 - sigmoid(X@theta.T))
    return -1 * np.mean(first + second)

6.2 Simplified Cost Function and Gradient Descent

【Cost Function 推导】

$J\left( \theta \right)=-\frac{1}{m}\sum\limits_{i=1}^{m}[y^{(i)}\log \left( h_\theta\left( x^{(i)} \right) \right)+\left( 1-y^{(i)} \right)\log \left( 1-h_\theta\left( x^{(i)} \right) \right)]$

代入函数

$h_\theta\left( x^{(i)} \right)=\frac{1}{1+e^{-\theta^Tx^{(i)}}}$

得到

$\begin{aligned} &y^{(i)}\log \left( h_\theta\left( x^{(i)} \right) \right)+\left( 1-y^{(i)} \right)\log \left( 1-h_\theta\left( x^{(i)} \right) \right)\\ =&y^{(i)}\log \left( \frac{1}{1+e^{-\theta^Tx^{(i)}}} \right)+\left( 1-y^{(i)} \right)\log \left( 1-\frac{1}{1+e^{-\theta^Tx^{(i)}}} \right)\\ =&-y^{(i)}\log \left( 1+e^{-\theta^Tx^{(i)}} \right)-\left( 1-y^{(i)} \right)\log \left( 1+e^{\theta^Tx^{(i)}} \right) \end{aligned}$

对函数进行求导

$\begin{aligned} &\frac{\partial }{\partial \theta_{j}}J\left( \theta \right)=\frac{\partial }{\partial \theta_{j}}[-\frac{1}{m}\sum\limits_{i=1}^{m}[-y^{(i)}\log \left( 1+e^{-\theta^{T}x^{(i)}} \right)-\left( 1-y^{(i)} \right)\log \left( 1+e^{\theta^{T}x^{(i)}} \right)]]\\ =&-\frac{1}{m}\sum\limits_{i=1}^{m}[-y^{(i)}\frac{-x_{j}^{(i)}e^{-\theta^{T}x^{(i)}}}{1+e^{-\theta^{T}x^{(i)}}}-\left( 1-y^{(i)} \right)\frac{x_j^{(i)}e^{\theta^Tx^{(i)}}}{1+e^{\theta^Tx^{(i)}}}]\\ =&-\frac{1}{m}\sum\limits_{i=1}^{m}[y^{(i)}\frac{x_j^{(i)}}{1+e^{\theta^Tx^{(i)}}}-\left( 1-y^{(i)} \right)\frac{x_j^{(i)}e^{\theta^Tx^{(i)}}}{1+e^{\theta^Tx^{(i)}}}]\\ =&-\frac{1}{m}\sum\limits_{i=1}^{m}\frac{y^{(i)}x_j^{(i)}-x_j^{(i)}e^{\theta^Tx^{(i)}}+y^{(i)}x_j^{(i)}e^{\theta^Tx^{(i)}}}{1+e^{\theta^Tx^{(i)}}}\\ =&-\frac{1}{m}\sum\limits_{i=1}^{m}\frac{y^{(i)}\left( 1\text{+}e^{\theta^Tx^{(i)}} \right)-e^{\theta^Tx^{(i)}}}{1+e^{\theta^Tx^{(i)}}}x_j^{(i)}\\ =&-\frac{1}{m}\sum\limits_{i=1}^{m}(y^{(i)}-\frac{e^{\theta^Tx^{(i)}}}{1+e^{\theta^Tx^{(i)}}})x_j^{(i)}\\ =&-\frac{1}{m}\sum\limits_{i=1}^{m}(y^{(i)}-\frac{1}{1+e^{-\theta^Tx^{(i)}}})x_j^{(i)}\\ =&-\frac{1}{m}\sum\limits_{i=1}^{m}[y^{(i)}-h_\theta\left( x^{(i)} \right)]x_j^{(i)}\\ =&\frac{1}{m}\sum\limits_{i=1}^{m}[h_\theta\left( x^{(i)} \right)-y^{(i)}]x_j^{(i)} \end{aligned}$

因此，我们得到同样的

$\theta_j := \theta_j - \alpha \frac{1}{m}\sum\limits_{i=1}^{m}{\left( h_\theta\left( x^{(i)} \right)-y^{(i)} \right)}x_{j}^{(i)}$

【Python 代码】

def gradient(theta, X, Y):
    
    return 1/len(X) *  (sigmoid(X @ theta.T) - Y) @ X

import scipy.optimize as opt

theta = opt.fmin_tnc(func=cost, x0=theta, fprime=gradient, args=(X, Y))
# model = opt.minimize(fun=cost, x0=theta, args=(X, Y), method='Newton-CG', jac=gradient)

# or

from sklearn.linear_model import LogisticRegression

model = LogisticRegression()
model.fit(X, Y)

6.4 Advanced Optimization

除了梯度下降算法以外，还有另外一些常被用来令代价函数最小的算法，这些算法更加复杂和优越，而且通常不需要人工选择学习率，比梯度下降算法要更加快速。这些算法有：共轭梯度（Conjugate Gradient），局部优化法(Broyden fletcher goldfarb shann,BFGS) ，有限内存局部优化法(LBFGS) ，变尺度法(Variable Metric Algorithm) 。

更多信息参考

6.5 Multiclass Classification_ One-vs-all

我们现在已经知道二元分类可以使用逻辑回归将数据集一分为二为正类和负类。而此分类思想也可以用在多类分类问题上。比如假设有三个类别，我们可以将其分成三个二元分类问题。最后，在我们需要做预测时，我们将所有的分类机都运行一遍，然后对每一个输入变量，都选择最高可能性的输出变量。

6.6 特征映射

$\operatorname{mapFeature}(x)=\left[\begin{array}{c}x_{1}^{0} x_{2}^{0} \\ x_{1}^{1} x_{2}^{0} \\ x_{1}^{0} x_{2}^{1} \\ x_{1}^{2} x_{2}^{0} \\ x_{1}^{1} x_{2}^{1} \\ x_{1}^{0} x_{2}^{2} \\ \vdots \\ x_{1}^{1} x_{2}^{5} \\ x_{1}^{0} x_{2}^{6}\end{array}\right]=\left[\begin{array}{c}1 \\ x_{1} \\ x_{2} \\ x_{1}^{2} \\ x_{1}^{1} x_{2}^{1} \\ x_{2}^{2} \\ \vdots \\ x_{1}^{1} x_{2}^{5} \\ x_{2}^{6}\end{array}\right]$

【Python 代码】

def feature_mapping(x, y, power, as_ndarray=False):
    
    data = {'f{0}{1}'.format(i-p, p): np.power(x, i-p) * np.power(y, p)
                for i in range(0, power+1)
                for p in range(0, i+1)
           }
    if as_ndarray:
        return pd.DataFrame(data).values
    else:
        return pd.DataFrame(data)
    
# 决策边界，thetaX = 0, thetaX <= threshhold
def find_decision_boundary(density, power, theta, threshhold):
    t1 = np.linspace(-1, 1.2, density)
    t2 = np.linspace(-1, 1.2, density)
    cordinates = [(x, y) for x in t1 for y in t2]
    x_cord, y_cord = zip(*cordinates)
    mapped_cord = feature_mapping(x_cord, y_cord, power)
    
    pred = mapped_cord.values @ theta.T
    decision = mapped_cord[np.abs(pred) <= threshhold]
    
    return decision.f10, decision.f01

7. Regularization

7.1 The Problem of Overfitting

到现在为止，我们已经学习了几种不同的学习算法，包括线性回归和逻辑回归，它们能够有效地解决许多问题，但是当将它们应用到某些特定的机器学习应用时，会遇到过拟合 (over-fitting) 的问题，导致它们效果很差。

就以多项式理解，$x$ 的次数越高，拟合的越好，但我们并没有足够的数据去约束这么多变量，导致相应的预测的能力就可能变差。

如果我们发现了过拟合问题，应该如何处理？

丢弃一些不能帮助我们正确预测的特征
- 可以是手工选择保留哪些特征
- 或者使用一些模型选择的算法来帮忙（例如PCA）
正则化
- 保留所有的特征，但是减少参数的大小（magnitude）

7.2 Cost Function

使用正则化的方法，我们可以手动对特定的系数添加惩罚项，即在代价函数中加入系数的平方。这个操作能减少变量过多的影响，但又不需要去除变量。

假如我们有非常多的特征，我们并不知道其中哪些特征我们要惩罚，我们将对所有的特征进行惩罚，并且让代价函数最优化的软件来选择这些惩罚的程度。这样的结果是得到了一个较为简单的能防止过拟合问题的假设：

$J\left( \theta \right)=\frac{1}{2m}[\sum\limits_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^{2}+\lambda \sum\limits_{j=1}^{n}\theta_{j}^{2}]$

$\lambda $又称为正则化参数（Regularization Parameter）, 如果选择的正则化参数$\lambda$ 过大，则会把所有的参数都最小化了，导致模型变成 $h_\theta( x )=\theta_{0}$，也就造成欠拟合。

7.3 Regularized Linear Regression

正则化线性回归的代价函数为

$J\left( \theta \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}[((h_\theta(x^{(i)})-y^{(i)})^{2}+\lambda \sum\limits_{j=1}^{n}\theta _{j}^{2})]$

如果我们要使用梯度下降法令这个代价函数最小化，因为我们未对$\theta_0$进行正则化，所以梯度下降算法将分两种情形：

$\theta_0:=\theta_0-a\frac{1}{m}\sum\limits_{i=1}^{m}((h_\theta(x^{(i)})-y^{(i)})x_{0}^{(i)})$ $\theta_j:=\theta_j-a[\frac{1}{m}\sum\limits_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_{j}^{\left( i \right)}+\frac{\lambda }{m}\theta_j]\text{ , for }j=1,2,...n$

我们同样也可以利用正规方程来求解正则化线性回归模型，方法如下所示：

$\theta=(X^TX+\lambda[\ 0\ I_0\ ])^{-1}X^Ty$

其中的 $[ 0 I_n]$ 为矩阵尺寸为 $(n+1)*(n+1)$，除了首行斜对角都为 1 的矩阵

If $\lambda>0$，对于严格对角占优矩阵 $X^TX+\lambda[ 0 I_0 ]$ 一定可逆

7.4 Regularized Logistic Regression

逻辑回归的代价函数增加一个正则化，得到

$J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}[-y^{(i)}\log \left( h_\theta\left( x^{(i)} \right) \right)-\left( 1-y^{(i)} \right)\log \left( 1-h_\theta\left( x^{(i)} \right) \right)]+\frac{\lambda }{2m}\sum\limits_{j=1}^{n}\theta _{j}^{2}$

要最小化该代价函数，通过求导，得出梯度下降算法为

【Python 代码】

def costReg(theta, X, y, learningRate):
    
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    first = np.multiply(-y, np.log(sigmoid(X*theta.T)))
    second = np.multiply((1 - y), np.log(1 - sigmoid(X*theta.T)))
    reg = (learningRate /2* np.mean(np.power(theta[:,1:theta.shape[1]],2))
    return np.mean(first - second) + reg
           
def regularized_gradient(theta, X, Y, learningRate=1):
           
    regularized_theta = learningRate / len(X) * theta[1:]
    regularized_term = np.concatenate([np.array([0]), regularized_theta])
    
    return  gradient(theta, X, Y) + regularized_term
           
# or
           
import scipy.optimize as opt
           
res = opt.minimize(fun=regularized_cost, x0=theta, args=(X, Y), method='Newton-CG', jac=regularized_gradient)

seaborn 是基于 matplotlib 的数据集分布可视化库。它在 matplotlib 的基础上，进行了更高级的封装，从而使得绘图更加容易，不需要经过大量的调整，就能使图像变得精致。

Machine Learning

#Supervised Learning #linear regression #Logistic Regression

【课程】吴恩达机器学习课程(一)

http://achlier.github.io/2022/08/03/吴恩达机器学习课程_1/

Author

Hailey

Posted on

August 3, 2022

Licensed under

【课程】吴恩达机器学习课程(二) Previous

【笔记】高等数学复习笔记-随机过程 Next